数値解析:フーリエ級数とフーリエ変換
現在工事中です。
フーリエ級数とフーリエ変換は、工学の各分野で数多く利用される汎用性のある、また応用性のある技術のひとつである。
純数学的な知識として身につける必要はまったくなく、単純に応用数学の世界で有効に利用できるテクニックのひとつと考え、
応用・利用できる程度の知識を身につければよい。
一般の多くの数学関数は、三角関数を用いた級数列の総和(すなわちフーリエ級数)で表すことができ、この性質を利用して、ある種の偏微分方程式の
解析解を導出することも可能である。
以下、フーリエ級数とフーリエ変換の基礎知識を紹介するとともに、工学への応用例を簡便に紹介する。
- 1. フーリエ級数とは
- 2. フーリエ級数の具体例
- 3. フーリエ積分
- 4. フーリエ変換
- 4.1変数分離法
- 4.2常微分方程式の解析解
- 4.3偏微分方程式の解析解
- 5. 偏微分方程式の解
- 6. 高速フーリエ変換
- 7. スペクトル法による流体解析
- 8. Literature Cited
【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。
フーリエ級数とは
工学の分野ではしばしばフーリエ級数とかフーリエ変換、高速フーリエ変換などの言葉が現れる。ここでは
フーリエ級数、フーリエ変換の初歩的な知見のみを紹介する。
工学的な解析技術のひとつとして、これらを自在に利用できる技術(テクニック)として覚えておくことは各方面で
応用技術として適用できる。純数学的な知見は数学屋に任せるとし、利用技術のみを身につけることが望ましい。
関数\(f(x)\ \)は\(x\ \)のすべての実数値に対し定義されていて、\(2 \pi\ \)を周期にもつとすると、 すなわち\(f(x+2 \pi)=f(x)\ \)。さらに、積分\( \int^\pi_{-\pi}|f(x)|dx\ \)が存在するとする。 いま、\(f(x)\ \)がつぎのように三角級数 \[ \begin{align*} f(x) = \frac{a_0}{2}+\sum^\infty_{n=1}(a_n \cos nx+b_n \sin nx) \tag{1'} \end{align*} \] で表されたとし、係数\(a_n,b_n\ \)と関数\(f(x)\ \)との間の関係を調べる。
(1)式の両辺に\( \cos mx\ \)をかけて、\(-\pi\ \)から\(\pi\ \)まで積分すると、 \[ \begin{align*} m=0のとき、& \int^\pi_{-\pi}f(x)dx=\pi a_0 \cr n \ne 0のとき、&\int^\pi_{-\pi}f(x) \cos mxdx=\pi a_m \quad (m=1,2,\cdots) \cr \end{align*} \] このとき、三角関数の直交性の積分公式を用いる。
同様に、(1)式の両辺に\( \sin mx\ \)をかけて、\(-\pi\ \)から\(\pi\ \)まで積分すると、 \[ \begin{align*} &\int^\pi_{-\pi}f(x) \sin mxdx=\pi b_m \quad (m=1,2,\cdots) \cr \end{align*} \] が得られる。
以上の結果から、\(2\pi\ \)を周期とする周期関数\(f(x)\ \)について、
\[
\begin{align*}
f(x) \sim \frac{a_0}{2}+\sum^\infty_{n=1}(a_n \cos nx+b_n \sin nx) \tag{1}
\end{align*}
\]
で表されるとき、係数\(a_n,b_n\ \)は、次式で与えられる。
\[
\left. \eqalign{
\begin{align*}
a_n & =\frac{1}{\pi}\int^\pi_{-\pi}f(x)\cos nxdx \quad (n=0,1,2,\cdots) \cr
b_n & =\frac{1}{\pi}\int^\pi_{-\pi}f(x)\sin nxdx \quad (n=1,2,\cdots) \cr
\end{align*}
} \right\} \tag{2}
\]
ここで、\(a_n,b_n\ \)を関数\(f(x)\ \)のフーリエ係数といい、これらを係数にもつ三角級数を
\(f(x)\ \)のフーリエ級数という。
(1)式で等号ではなく記号\(\sim\ \)を用いたのは級数の収束条件が成り立たない可能性が少ないながらもあるためである。
多くの場合には等号と見なしても差し支えない。以下の数式にも同じ意味で\(\sim\ \)を使っている。
周期\(2\pi\ \)でなく、一般の周期\(2L\ \)をもつ周期関数\(f(x)\ \)についても、新しい変数\(t\ \)として \[ t=\frac{\pi}{L}x \tag{3} \] と変換すれば、\(f(\frac{\pi}{L}x)\ \)は周期\(2\pi\ \)をもち、(1)(2)式と類似の式(5)(6)を導くことができる。 \[ \begin{align*} f(x) & \sim \frac{a_0}{2}+\sum^\infty_{n=1}(a_n \cos \frac{n\pi}{L}x+b_n \sin \frac{n\pi}{L}x) \tag{4} \end{align*} \] \[ \left. \eqalign{ \begin{align*} a_n & =\frac{1}{L}\int^L_{-L}f(x)\cos \frac{n\pi}{L}xdx \quad (n=0,1,2,\cdots) \cr b_n & =\frac{1}{L}\int^L_{-L}f(x)\sin \frac{n\pi}{L}xdx \quad (n=1,2,\cdots) \cr \end{align*} } \right\} \tag{5} \]
フーリエ級数の具体例
大概の周期関数は、フーリエ級数で表すことが可能である。その適用例をいくつか紹介し、フーリエ級数のおおよその概念を掴んで頂きたい。
関数\(f(x)\)は、範囲\([-\pi,\pi]\)の周期関数となっている。(2),(3)式に代入すると、 \[ \begin{align*} a_n & =-\frac{1}{\pi}\int^0_{-\pi}\cos nxdx+\frac{1}{\pi}\int^\pi_0\cos nxdx=0 \quad (n=0,1,2,\cdots), \cr b_n & =-\frac{1}{\pi}\int^0_{-\pi}\sin nxdx+\frac{1}{\pi}\int^\pi_0\sin nxdx, \cr & = \left\{ \eqalign{ & 0 \quad (n=2,4,\cdots), \cr & \frac{4}{n\pi} \quad (n=1,3,5,\cdots) } \right. \tag{7} \end{align*} \] したがって、これらをフーリエ級数、(1)式に代入し整理すると、次式が得られる。 \[ \begin{align*} f(x) & \sim \frac{4}{\pi}\sin x+ \frac{4}{3\pi}\sin 3x+\cdots =\frac{4}{\pi}\sum^\infty_{n=1} \frac{\sin(2n-1)x}{2n-1} \tag{8} \end{align*} \]
フーリエ級数(8)式で、総和の部分和\(n=1,n=2,n=3,n=10\)までとしたときの関数値をプロットすると、下の図1
のように表される。
級数の和を大きくすることで、もとの関数\(f(x)\)に次第に漸近していることが理解できる。
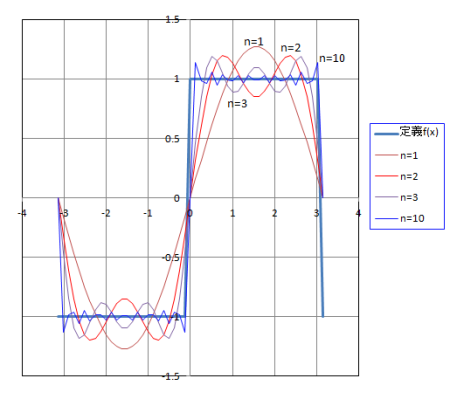
図1:Fourier級数の例
区間[\(-\pi,\pi\)]で考えると、\(f(-x)=-f(x)\)で奇関数であるからフーリエ級数は正弦級数となる。 単純に公式に当てはめる。まず係数\(a_n\)は、定積分するとゼロとなる。\(x \cos nx \)の不定積分を参考までに記載している。 \[ \begin{align*} a_n & =\frac{1}{\pi}\int^\pi_{-\pi}x \cos nxdx, \quad (n=0,1,2,\cdots) \cr & = 0 \tag{10} \cr \int x \cos nxdx & = {1 \over n} x \sin nx - {1 \over n} \int \sin nxdx, \cr & = {1 \over n} x \sin nx + {1 \over n^2} \cos nx \cr \end{align*} \] また、係数\(b_n\)も同様に、定積分すると次のようになる。参考に不定積分および三角関数の性質を記載している。 \[ \begin{align*} b_n & =\frac{1}{\pi}\int^\pi_{-\pi}x \sin nxdx, \quad (n=1,2,\cdots) \cr & = {-1 \over n} 2\pi \cos n\pi, \cr & = (-1)^{n-1} \frac{2\pi}{n} \tag{11} \cr \int x \sin nxdx & = {-1 \over n} x \cos nx + {1 \over n} \int \cos nxdx, \cr & = {-1 \over n} x \cos nx + {1 \over n^2} \sin nx \cr \cos (-nx) & = \cos nx, \cr \sin (-nx) & = -\sin nx \cr \end{align*} \] したがって、フーリエ級数は \[ \begin{align*} f(x) \sim 2\sum^\infty_{n=1} (-1)^{n-1} \frac{\sin nx}{n} \tag{12} \end{align*} \] となる。ちなみに岩波全書の「数学公式II」1)に各種周期関数のフーリエ級数がリストされている。
フーリエ積分
無限区間で周期を持たない関数を三角関数の積分で表そうとするとき、有限区間[-L,L]のフーリエ級数で表し、 この区間\(L \rightarrow \infty \ \)と極限をとることで、次の積分形で表される。 \[ \begin{align*} f(x) & \sim \int^\infty_0A(\alpha)\cos \alpha x d\alpha+\int^\infty_0B(\alpha) \sin \alpha x d\alpha, \tag{13} \cr \end{align*} \] 右辺を\(f(x)\)のフーリエ積分という。 ここで、積分の中の\(A(\alpha),B(\alpha)\)は、 \[ \begin{align*} \left. \eqalign{ A(\alpha) & =\frac{1}{\pi}\int^\infty_{-\infty}f(u)\cos \alpha udu, \cr B(\alpha) & =\frac{1}{\pi}\int^\infty_{-\infty}f(u)\sin \alpha udu } \right. \tag{14} \end{align*} \] で表される。
更に(14)式を(13)式に代入して変形すると、 \[ \begin{align*} f(x) & \sim \frac{1}{\pi}\int^\infty_0 \int^\infty_{-\infty}f(u)\cos \alpha(x-u)dud\alpha \tag{15} \end{align*} \] が得られる。これもフーリエ積分という。
フーリエ変換
更に複素形フーリエ級数に対応するフーリエ積分を求めると \[ \begin{align*} \left. \eqalign{ f(x) & \sim \frac{1}{\sqrt{2\pi}} \int^\infty_{-\infty}F(\alpha)e^{i \alpha x}d\alpha, \cr F(\alpha) & = \frac{1}{\sqrt{2\pi}} \int^\infty_{-\infty}f(u)e^{-i \alpha x}du } \right. \tag{16} \end{align*} \] が得られる。(16)式の\(F(\alpha)\ \)を\(f(x)\)のフーリエ変換という。
(16)式の\(f(x)\ \)が偶関数のとき、 \[ \begin{align*} \left. \eqalign{ f(x) & \sim \sqrt{\frac{2}{\pi}}\int^\infty_0 C(\alpha) \cos \alpha x d\alpha \cr C(\alpha) & =\sqrt{ \frac{2}{\pi}}\int^\infty_0 f(u)\cos \alpha udu } \right. \tag{17} \end{align*} \] 同じく、(16)式の\(f(x)\ \)が奇関数のとき、 \[ \begin{align*} \left. \eqalign{ f(x) & \sim \sqrt{\frac{2}{\pi}}\int^\infty_0 S(\alpha) \sin \alpha x d\alpha \cr S(\alpha) & =\sqrt{ \frac{2}{\pi}}\int^\infty_0 f(u)\sin \alpha udu } \right. \tag{18} \end{align*} \] と表される。\(C(\alpha)\)をフーリエの余弦変換、\(S(\alpha)\)をフーリエの正弦変換という。
以上でフーリエ級数、フーリエ変換の基礎的な知見であり、工学的にこれらを応用・利用するための基礎知識といえる。
工学分野では、いろいろな微分方程式、偏微分方程式が現れ、ときとして解析解が求められる場合もある。古い論文などの
電子計算機が出現する以前は、これら微分方程式を解析的に求めることが行われていた。
解析解を導出するときのスマートさに筆者は憧れ、フーリエ変換とかラプラス変換などの求解のための技術を
独習で身につけたものです。これら理論的な背景を知らなくても、求解のためのテクニックとを知っておくことが大切である。
フーリエ変換のひとつに、高速フーリエ変換(Fast Fourier Transform,FFT)というのがあり、特に計測分野では波形処理・スペクトル解析でよく利用される。
偏微分方程式
偏微分方程式の形によっては、変数分離法により、常微分方程式に変換できる。また与えられた境界条件・初期条件は フーリエ級数に変換することができ、もとの偏微分方程式の解析解を求めることができる。
変数分離法
ここでは工学的に頻出する熱伝導の式、拡散の式と呼ばれる偏微分方程式を例にとり、その解析解を導出する。
\(y(x,t)=X(x)T(t) \ \)とおいて、与えられた偏微分方程式に代入する。 \[ \begin{align*} \left. \eqalign{ X(x)T'(t) & =kX''(x)T(t), \cr \frac{T'(t)}{kT(t)} & = \frac{X''(x)}{X(x)} } \right. \tag{21} \end{align*} \] 最後の式の左辺は\(t \ \)のみの関数、右辺は\(x \ \)のみの関数であるから、両辺はある定数でなければならない。 両辺をある定数\(-\lambda^2 \ \)に等しいとおくと、次の2つの常微分方程式が得られる。 \[ \begin{align*} X''+ \lambda^2 X & =0, \tag{22} \cr T' + k \lambda^2 T & =0 \tag{23} \end{align*} \] ここまでで、変数分離法により、偏微分方程式が2つの常微分方程式に変換できたことになる。
常微分方程式の解析解
常微分方程式の(22)式の一般解は、 \[ \begin{align*} \lambda^2 >0, \quad X(x) & =A \cos (\lambda x)+B \sin( \lambda x),\tag{24a}\cr \lambda^2 =0, \quad X(x) & =Ax+B, \tag{24b} \cr \lambda^2 <0, \quad X(x) & =A \cosh (-\lambda x)+B \sinh( -\lambda x) \tag{24c} \cr \end{align*} \] となる。ここで\(A,B \ \)は積分定数。境界条件\(y(0,t)=0,y(2,t)=0\ \)の周期性を考えると、一般解の\(\lambda^2>0\ \)の場合の解(24a)以外にない。 また境界条件\(X(0)T(t)=0,\ X(2)T(t)=0\ \)から、\(X(0)=0,\ X(2)=0\ \)ゆえ、\(B \ne 0\ \)とすれば \[ \begin{align*} X(0) & = A \cos 0 + B \sin 0, \cr & = A =0, \tag{25a} \cr X(2) & = B \sin 2 \lambda =0, \cr 2 \lambda & = n \pi, \quad (n=1,2,\cdots) \tag{25b} \end{align*} \] を得る。
一方、常微分方程式(23)式の一般解は、 \[ \begin{align*} T(t) = ce^{-k \lambda^2 t} \tag{26} \end{align*} \] となる。\(c\ \)は積分定数。
偏微分方程式の解析解
したがって、偏微分方程式の解は、積分定数を\(c_n\ \)とすると、 \[ \begin{align*} y(x,t)=\sum^\infty_{n=1} c_n e^{-\frac{kn^2\pi^2}{4}t} \sin \frac{n\pi}{2}x \tag{27} \end{align*} \] となる。
次に初期条件\(y(x,0)=x \ \)を利用して、積分定数\(c_n \ \)を求めることを考える。 初期条件右辺の関数\(x\ \)を区間[0,2]でフーリエの正弦級数で表すとすれば、 \[ \begin{align*} y(x,0)=x &=\sum^\infty_{n=1} b_n \sin \frac{n\pi}{2}x,\tag{28a} \cr b_n & =(-1)^{n-1}\frac{4}{n\pi} \tag{28b} \end{align*} \] となる。\(t=0\ \)を代入した(27)式と(28)式とを比較すると \[ \begin{align*} c_n=b_n \tag{29} \end{align*} \] となる。故に与えられた偏微分方程式の与えられた境界条件を満足する解は、 \[ \begin{align*} y(x,t)=\sum^\infty_{n=1} (-1)^{n-1}\frac{4}{n\pi} e^{-\frac{kn^2\pi^2}{4}t} \sin \frac{n\pi}{2}x \tag{30} \end{align*} \] と求められる。
偏微分方程式を解析的に解くとき、変数分離して、常微分方程式に変換する。そしてこの常微分方程式の解析解を求める。 さらに、初期条件または境界条件をフーリエ級数で表すことにより、オリジナルの偏微分方程式の解析解が得られる。
高速フーリエ変換
フーリエ変換では、時間領域を周波数領域に変換し、周波数領域での各種操作をしたのち、逆変換しもとに戻すという操作を行う。
通常、デジタル信号処理や波形処理など連続または離散波形を処理するときに利用される。
高速フーリエ変換(Fast Fourier Transform, FFT)はCooley and Tukeyにより提唱され、計算時間を劇的に短縮できる。
筆者は、非定常細線法と呼ばれる液体の熱伝導度測定実験をしたことがある。
白金などの金属細線を液体中に浸し、細線に電流を流す。このとき細線が発熱し、周囲の液体に熱を伝導する。
熱の伝導が速いと細線の温度上昇は緩くなる。温度上昇を細線の電気抵抗で測定することで、温度上昇速度
を測り、最終的に液体の熱伝導度を測定しようとする方法である。
実験では1秒間で1000回の速さ(1kHz)で電気抵抗値(実際には電圧)をサンプリングする。ほぼ2,3秒経つと液体中に対流が発生し、正確な熱伝導度を測定出来なくなる。 したがって実験開始から数秒の間だけ、データをサンプリングすることになる。
PCにてサンプリングした生データの一例を図2に示す。横軸は時間の自然対数\( \ln t\ \)、縦軸はブリッジの電圧(抵抗値の変化をダブルブリッジの非平衡電位で測定)の時間変化を示す。
この生データには、周期ノイズが重畳しているが、必要なデータは図中にフィッティングしている直線部分の傾きが熱伝導度の算出に必要となる。
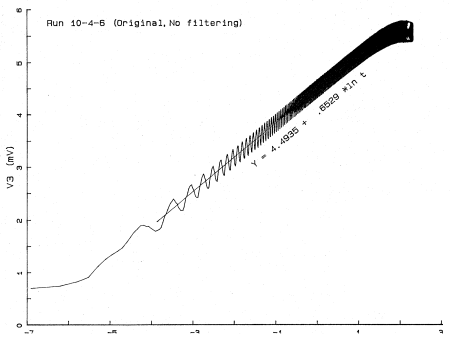
図2:非定常細線法によるサンプリングした生データ
フーリエ変換することで、周波数領域に変換すると、およそ60Hzの商用電源の周波数成分(ノイズ)が乗っていることが判明した。
実際には大学の古い実験建屋にて実験していたため、電源周波数成分のノイズを拾っていた。
そこで、フーリエ変換したのち、周波数領域60±1Hzのバンドカットフィルターでノイズを除去し、逆フーリエ変換すると、
下の図3のような、多少まだノイズが乗っているが、かなり改善されていることが分かる。
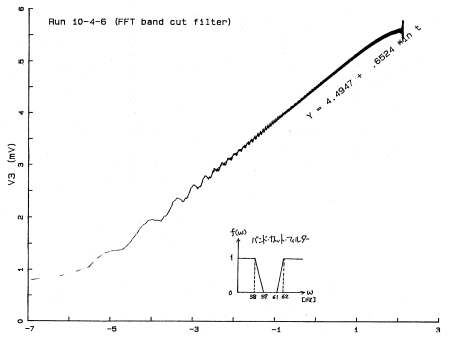
図3:フーリエ変換で60Hz成分をカットした後
この例では1kHzのサンプリング周期であり、連続して測定しておらず、離散型フーリエ変換(Discrete Fourier Transform, DFT)を利用している。 特に高速フーリエ変換(FFT)アルゴリズムで計算を飛躍的に短縮する方法が図書3)などに紹介されていて、Sande-TukeyによるFFTアルゴリズムを採用し、実験データの 信号処理に利用した。
スペクトル法による流体解析
気象庁の全球モデル(Global Spectral Model)と呼ばれる、地球全体の大気を数値予報するモデルは
差分法ではなく、スペクトル法が使われている。全球モデルについては、気象庁のホームページを参照されたい。
スペクトル法による流体解析の経験は筆者にはないので詳細は割愛する。
Literature Cited
本ページを作成するにあたって、以下の書籍を参考にした。
- 参考文献
- 1) 森口、宇田川、一松著:「数学公式I,II,III」、岩波全書(1979).
- 2) 矢野、石原著:「解析学概論」、裳華房(1971).
- 3) 南 茂夫著:「科学計測のための波形データ処理」、CQ出版社(1986).
- 4) 日野幹雄著:「スペクトル解析」、朝倉書店(1988).
- 5) 間宮、西川著:「化学計測のためのフーリエ変換法入門」、共立出版(1983).
