数値解析:線形方程式
現在工事中です。 工学系のシミュレーションで最も利用頻度の高い数学ルーチンであると思われる連立線形方程式の解法について解説する。 流体解析をはじめとする大規模な連立線形方程式の解法は、計算時間の短縮を目指し、高速化が今なお図られている。高速化のために現有のマルチCPUコアを有効利用するための世界的な標準化(たとえばOpenMP)も順次行われている。 ここでは1990年代からのベクトル計算機(スパコン)時代から現代のマルチコアCPUの連立一次方程式の計算速度について、ユーザーの立場に立っての検討を実施している。
- 1. 線形方程式の概要
- 2. 直接法による線形方程式の解法
- 3. 計算時間の比較
- 3.1 32ビット環境の速度比較
- 3.2 64ビット環境の速度比較
- 3.3 Intel MKLライブラリの速度比較
- 4. 連立一次方程式の解法(バンド行列のとき)
- 5. 連立一次方程式を解くときの注意事項
- 5.1 連立一次方程式のスケーリング
- 5.2 係数行列の正則判定
- 6. 解法の高速化
- 7. Literature Cited
【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。
線形方程式の概要
工学分野の数値解析においてもっとも頻繁に利用されるサブルーチンである、線形方程式系の解法について以下紹介する。 「線形方程式系」と"系" をつけたのは"System"という意味で連立、"線形" すなわち一次の連立方程式を指している。
このページでは n元の連立一次方程式、 \[ \begin{align*} {\bf A}{\bf x} = {\bf b} \tag{1} \end{align*} \]
の一般的な解法について説明する。ここで\( {\bf A} \)は n次の正方行列、\( \bf x \)は解ベクトル、\( \bf b \)は定数項ベクトルである。
連立一次方程式の解法には、大別して次の2つがある。
- 1) 直接法(式の変形により厳密解を求める)
- 2) 間接法(反復法とも呼ぶ。反復的に計算し、近似解を求める)
直接法には、Gaussの消去法、Gauss-Jordanの掃出し法、LU分解による方法がある。間接法にはJacobi反復法、Gauss-Seidel法、共役勾配法がある。
また係数行列がフルに要素を持っていたり、対称行列であったり、バンド行列であったり、スパースな行列であったりと、係数行列の性質により 得意な解法が用意されている場合がある。得意とは高速解法であったり、省メモリであったり、並列計算向けであったりすることである。
係数行列が固定で、右辺の定数項ベクトルだけが種々変動する場合を解くなどの場合にも、解法によっては高速に解ける場合もある。
流体解析のときは、巨大な連立一次方程式を解くことが計算の大部分を占めることはよく知られており、大規模な連立方程式を短時間で解くための各種 工夫が行われている。マルチCPUによる並列化、マルチグリッドによる並列化(スパコン)など用途は広い。
流体解析以外の、化学工学分野では反応器シミュレーション(非線形連立方程式を解く)など流体解析に近い大きさの問題を解くこともあり、こうしたシミュレーション でも連立一次方程式の高速、省メモリ解法が求められている。 非線形方程式の解法のところでも述べたように、Newton法などを用いるとき線形近似を行い連立の線形方程式に帰着させて解く操作を実施し、これを反復することで非線形方程式の解を得る。したがって連立の線形方程式の解法の計算が全体の計算時間の大きな割合を占めることになり、解法の高速化・並列化が望まれる。
以下、図書などに記載されている連立一次方程式のコードについての知見(計算速度など)を詳述する。
直接法による線形方程式の解法
図書、インターネットで利用可能な連立一次方程式の解法コードの例を次のリストに示す。 1)から9)まではソースがFortranベースのコード、10),11)はC言語のコードである。また8)はIntel Fortranのライブラリ(MKL)として提供されており、ソースコードは開示されていない。 MKL以外のコードは開示されている。リストに示す名称はサブルーチン名をそのまま採用した(あるいはわたしが勝手に名付けたルーチン名を示す)。
- 1. SAXGLU1)
- 2. USAXGL1)
- 3. WSAXGL1)
- 4. LU222)
- 5. BGAUSS2)
- 6. DLINLU3)
- 7. USHIJM4)
- 8. DGETRF+DGETRS(MKL-LIB)
- 9. DGETRF+DGETRS(LAPACK)
- 10. LEQ5)
- 11. LEQACC5)
リストアップしたルーチンの多くは出典がいずれも古い(1990年代の大型スパコンの時代のもの)。逆に新しいソースコードはその後、知財関連の権利保護のため公表されなくなっているように思う。 なお上付添字番号は、末尾の文献番号を示す。
解法の簡単な概要を表1に示す。ただしLU分解部分の概要のみを記した。またLU分解後の後退代入はいずれのルーチンもほぼ同じ。
| コード名 | 出典 | 概要 |
|---|---|---|
| SAXGLU | 1) | 内積形式ガウス消去法に基づくLU分解法 |
| USAXGL | 1) | 内積形式ガウス消去法に基づくLU分解法(ループアンローリングを施す) |
| WSAXGL | 1) | 内積形式ガウス消去法に基づくLU分解法(同上+文の入換え) |
| LU22 | 2) | 内積形式ガウス消去法に基づくLU分解法(2列同時2列消去法) |
| BGAUSS | 2) | 内積形式のたてブロックガウス法によるLU分解法 |
| DLINLU | 3) | ガウス消去法によるLU分解法 |
| USHIJM | 4) | 部分ピボット選択を利用するLU分解法 |
| mkl-LIB | 6) | 部分ピボット選択を利用するLU分解法 |
| LAPACK | 7) | 部分ピボット選択を利用するLU分解法 |
| M_LEQ | 5) | 完全ピボット選択を利用するガウス消去法 |
| M_LEQACC | 5) | 完全ピボット選択を利用するガウス消去法に基づくLU分解法 |
計算時間の比較
上の連立一次方程式の解法ソースコードを、計算速度の観点から比較を実施する。
32ビット環境の速度比較
計算速度は、計算機環境に大きく依存するため、まず32ビットアプリケーションとしてコンパイル・リンクし、連立一次方程式を解いた。
解法ルーチンの計算時間を比較するため、使用するコンパイラーの最適化オプション、起動するマシンのCPU性能、マルチCPU、並列化仕様などテスト環境に大きく依存する。 計算速度の計測の結果の例を、表2に示すが、使用したマシンは、Intel i7 (core 7, 920, 2.67GHz)、4コア、HTで、OSはWindows 7(64bit Ed.)、物理メモリ8GBにて実施。 コンパイラーは Intel Visual Fortran(IVF) 13.1.1.171を用い、32bitアプリとしてコンパイルし、コンパイラー・オプションは、"/O3 /Qparallel /Zi /Qpar-report1"を用いた。OpenMPによる並列化は実施していない。 コンパイラーによる自動並列化"Qparallel"のみ適用。
| ルーチン名 | N=1000 | N=2000 | N=4000 | N=5000 |
|---|---|---|---|---|
| LU22 | 410 | 3050 | 23240 | 44660 |
| SAXGLU | 460 | 3860 | 32990 | 63810 |
| USAXGL | 370 | 3560 | 28120 | 53830 |
| WSAXGL | 340 | 2360 | 18430 | 35280 |
| BGAUSS | 390 | 3720 | 32310 | 62760 |
| DLINLU | 960 | 11030 | 116130 | 235640 |
| USHIJM | 500 | 4940 | 40680 | 78910 |
| mkl-LIB | 210 | 1010 | 7710 | 14830 |
| LAPACK | 450 | 4860 | 40330 | 78580 |
| M_LEQ | 1270 | 11600 | 94180 | 183010 |
| M_LEQACC | 5840 | 58900 | 515760 | 1021520 |
なお上表の計算時間は連立一次方程式のルーチンに入ってから出るまでの時間を計測しており、係数行列の設定や解ベクトルの出力などは含まれていない。またルーチンの途中出力は基本的にない。 Windows 7上のCommand Promptから実行しており、当然フォアグラウンドで起動しているが、バックグラウンドでほかのジョブは走っている。そのため計算時間には誤差や機差が含まれる。
計測のためのメインルーチンの抜粋をリスト1に示す。
リスト1から、IND=8のときのインテルのMKL(Math Kernel Library)でDGETRFを最初に呼び出しLU分解を行い、次にDGETRSにより解ベクトルを求めている。これらルーチンは LAPACKに同名のルーチンがあり、インテルが独自にライブラリ化したものである。 なおMKLライブラリは、次のオプションを用い、リンクしている(並列化バージョンではなく、シーケンシャル版)。
#### static link, sequential version, cdecl
LIBMKL= mkl_intel_c.lib mkl_sequential.lib \
mkl_core.lib
IND=9で、LapackのソースをIVFでコンパイルしたものを比較している。 またIND=10、11はC言語ソースをIntel C++でコンパイルし、Fortranルーチンから呼び出している。複数の言語の混在利用についてはインテル社マニュアルを参照されたい。
表2の結果を、横軸に行列の次元数Nを、縦軸に計算時間[ms]をとり片対数プロットしたものを図1に示す。
図1:計算速度の比較
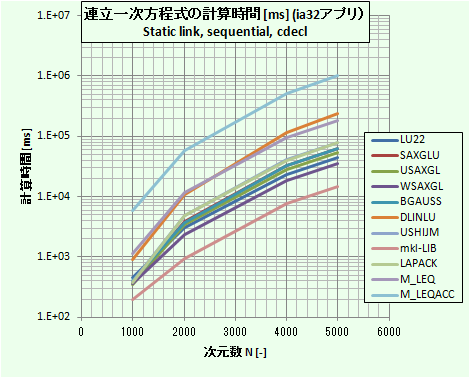
図1(表2からもわかるが)からわかるように、IntelのMKLライブラリにあるルーチンがダントツに速く、C言語ソースのルーチン(M_LEQ、M_LEQACC)はもっとも遅い。ほかのFortranルーチンは計算速度に幅があり、その中でWSAXGLルーチンが最も速い。
特徴的なのは、LAPACKのFortranソースからコンパイルリンクしたルーチン(Intel MKLライブのルーチンと中身は同等)はそれほど速くなく、むしろ遅い方に分類される。 ということから、IntelのMKLライブラリは高速化を図るためにLAPACKの中身まで踏み込んだ改良を実施しているものと予想される。
64ビット環境の速度比較
同じ例題1を、64ビットアプリケーションとしてコンパイル・リンクし、連立一次方程式を解き、計算時間を比較した。
計算時間を表3に、また横軸に次元数縦軸に計算時間の片対数プロットしたものを図2に示す。
| ルーチン名 | N=1000 | N=2000 | N=4000 | N=5000 |
|---|---|---|---|---|
| LU22 | 440 | 2740 | 23160 | 44980 |
| SAXGLU | 450 | 3920 | 33530 | 64870 |
| USAXGL | 360 | 3600 | 28220 | 54360 |
| WSAXGL | 330 | 2470 | 18560 | 35940 |
| BGAUSS | 400 | 3790 | 32760 | 64010 |
| DLINLU | 940 | 10930 | 118280 | 239600 |
| USHIJM | 360 | 5120 | 41500 | 83620 |
| mkl-LIB | 160 | 910 | 7200 | 14080 |
| LAPACK | 400 | 5030 | 41110 | 80430 |
Intel MKLライブラリをリンクするときのライブラリ指定は次のライブラリを使用した。
##### static link, sequential version, LP64
LIBMKL= mkl_intel_lp64.lib mkl_sequential.lib \
mkl_core.lib
図2:計算速度の比較(64bitアプリ)
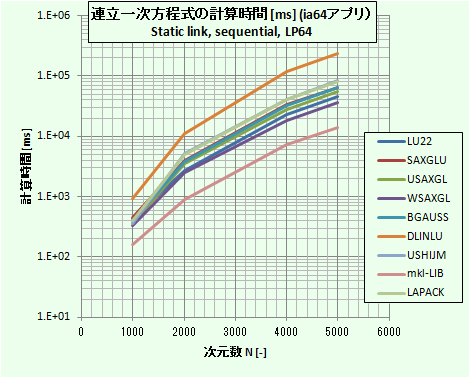
表3および図2から、64ビットアプリとしてもほとんど計算時間の順番は変わっておらず、IntelのMKLライブラリのルーチンが最も速い。次いでWSAXGLが2番目に速い。 Intel MKLライブラリのルーチンについては、64bitアプリの方が32bitアプリより約10%程度速い結果が得られている。
なお、C言語ソースの解法は割愛した。
Intel MKLライブラリの速度比較
Intel MKLライブラリの連立一次方程式の解法は、LAPACKルーチンを基本としているが、Sequential VersionとParallel Version、Static Library VersionとDynamic Library Versionなどと組み合わせがあり、32bitと64bitの組み合わせを含め、23=8 種類以上がある。 ここではこれら組み合わせたときの速度比較を実施した。同じく例題1を計算例として採用した。計算時間を表4に、同じく図3に計算時間をプロットした。
| 次元数 N | 1000 | 2000 | 4000 | 5000 |
|---|---|---|---|---|
| 32bit,Static,Parallel | 100 | 310 | 2360 | 4410 |
| 32bit,Dynamic,Parallel | 390 | 320 | 2580 | 4300 |
| 32bit,Static,Sequential | 210 | 1010 | 7710 | 14830 |
| 32bit,Dynamic,Sequential | 200 | 960 | 7650 | 14840 |
| 64bit,Static,Parallel | 80 | 380 | 2220 | 4640 |
| 64bit,Dynamic,Parallel | 380 | 400 | 2420 | 4360 |
| 64bit,Static,Sequential | 160 | 910 | 7200 | 14080 |
| 64bit,Dynamic,Sequential | 270 | 920 | 7300 | 14060 |
図3:計算速度の比較(Intel MKLルーチン)
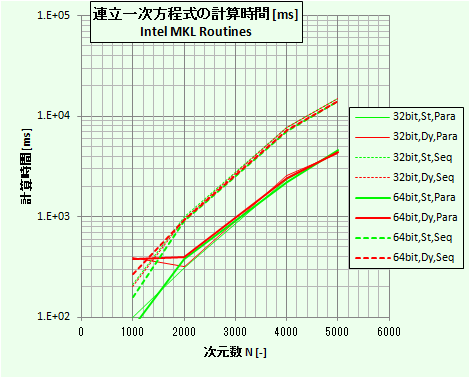
N=1000のとき計算時間にばらつきが見られ、誤差が含まれている様子が見える(バックグラウンドジョブの影響かも)。
しかし、Nが大きいとき図3から、Parallel Versionの方がSequential Versionに比べ計算速度が約1/3に減少している。 Dynamic LibraryとStatic Libraryとでは顕著な差はみられない。 32bit Versionと64bit Versionとでは、約5-10%程度64bit Versionの方が速い。
連立一次方程式の解法では、Intel MKLルーチンが圧倒的に速いことが分かる。 ただし、ユーザー側からするとソースコードがブラックボックス化しており、万が一の場合の不安が残る。非線形方程式を線形化し反復解法を適用するとき収束性に問題が発生した時などデバッグ時にソースコードがない(MKLライブラリはLibファイルの提供のみでソースは公開されていない)こと が欠点といえば欠点と考えられる。ユーザー側からすれば利用しづらい。
連立一次方程式の解法(バンド行列のとき)
これまでは行列として非対称フルマトリックスの解法を解説してきた。ここでは化学工学で頻繁に現れるバンドマトリックス(帯行列)の連立一次方程式の解法について解説する。
蒸留計算のように、段(Tray)上の気液の収支式はその段の上下段のみの関数であり、行列で表すと対角要素とその前後の要素だけが要素として現れ、ほかはすべてゼロとなるバンドマトリックスで記述できる。
また反応器モデルの混合拡散モデルでも、基礎式である微分方程式を差分に置き換えると、ある要素とその直前・直後の要素だけが現れる、バンドマトリックスとなる。
バンドマトリックスを持つ連立一次方程式の計算速度の比較は、 ここ(未リンク)で行なうので参照されたい。
連立一次方程式を解くときの注意事項
化学工学計算や反応器シミュレーションでは、物質収支式、熱収支式、圧力収支式を同時に連立して解くことが多い。また流体解析では運動量収支式(Navier-Stokes式)を同時に解くことを行う。こうした支配方程式は多くは非線形であり、 線形化し、反復により収束計算を行う。
連立一次方程式のスケーリング
化学工学では独立変数を無次元化し、無次元数を用いて計算を実施することもあるが、デバッグなどの変数の理解し易さから直接、有次元数を変数として採用することが多い。 有次元数を用いると、使用する単位系によっては得られる連立一次方程式の両辺をスケーリングし、得られる解の精度が同等になるよう調整を行う必要がある(場合がある)。
係数行列の正則判定
連立一次方程式を解くとき、正則判定条件を緩くすると、正則判定条件にひっかかり計算が進まなくなることがある。 標準的な判定条件3)として、単精度では10-5、倍精度では10-14を推奨しているが、 計算状況を見て、適宜、変更する必要がある。行列が正則と判定されるとき基礎式のダブり(数学的に不定となる基礎式を選択していないか)にも注意が必要である。
解法の高速化
流体解析をはじめとする非線形方程式の解法では、線形化を行い、連立一次方程式に変換し、反復計算を実施している。未知変数が数万から数十万、場合によっては数百万となることも珍しくない。流体解析で計算時間の大部分を占めるのが連立一次方程式の解法部分であることは良く知られている。
連立一次方程式を高速に解くことができれば、全体の計算時間の短縮に直結し、ターンアラウンドの改善となる。連立一次方程式の解法の高速化には、OpenMPによる並列化手法が現在では一般的となっている。もちろんコンパイラーによる自動並列化も手段としてはあるが、きめ細かい高速化にはOpenMPのコマンドを埋め込む手法が手っ取り早い。
連立一次方程式のOpenMPによる高速化については、数値解析:OpenMPによる高速化(未リンク)で解説するので参照されたい。
OpenMPをはじめとする並列化の一般知識については、ここ、計算機:並列化(未リンク)を参照されたい。
Literature Cited
- 引用文献・参考図書
- 1) 島崎著:「スーパーコンピュータとプログラミング」、共立出版(1989).
- 2) 村田、小国、唐木著:「スーパーコンピュータ」、丸善(1986).
- 3) 渡部、名取、小国著:「数値解析とFORTRAN」第3版、丸善(1983).
- 4) 牛島著:「OpenMPによる並列プログラミングと数値計算法」、丸善(2006).
- 5) 戸川隼人著:「新装版 科学技術計算ハンドブック基礎篇C言語版」、サイエンス社(2002).
- 6) インテル:マス・カーネル・ライブラリー(Intel MKL).
- 7) LAPACK:Linear Algebra PACKage, Netlib(www.netlib.org).
