トップ > ライブラリ > 技術計算 > 反応器シミュレーション

技術計算：反応器シミュレーション

現在工事中です。 取り敢えず繋がりましたが、まだまだ未完成（これからも更新する予定）です。

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

先頭に戻る

反応器シミュレーション概要

化学工業における新規プロセスの開発は、新製品（化学品）を如何に効率良く製造できるプロセスを創造し構築することである。特にその開発の中心は 反応器の開発と言っても過言ではない。反応器の前後の工程である原料調合や分離・精製といった工程はほぼ確立した単位操作であり、それほど開発の 重点が置かれることは少ない。

反応器シミュレーションができるように体制を整えることは、反応器の開発や反応器の設計、スケールアップに必要不可欠なステップである。化学反応のルートや速度量論 （反応モデル）がラボスケールでほぼ求められており、開発に用いたテスト試験装置の内部の流動・混合モデル（反応器モデル）がほぼ予測できる状況になって、本格的なシミュレーションを 行うための必要条件である。シミュレーションによる更なるチューニングを実施できるようにツールを整備する必要がある。

反応器シミュレーションに限らず、通常のプロセスシミュレーションでは計算の安定性が要求される。どんな入力条件でも安定して解が得られ、そこそこの計算精度が得られることが必須である。 計算精度とは、スケールアップのように反応器サイズが異なった入力データに対してもほぼ妥当な計算結果を与える反応モデル、反応器モデルにまでブラッシアップする必要があり、ベンチ試験、パイロット試験 の進行とともにシミュレータの計算精度も向上させていかなければならない。

次に多くのケーススタディを実行するため、計算時間の短縮が要求される。反応速度パラメータ（頻度因子や活性化エネルギー）をラボ試験のデータから求めるが、ベンチ試験・パイロット試験 のデータでもこれらパラメータをチューニング・最適化することがよく行われる。このとき、ここで作成した反応器シミュレータを中核とした、最適化ループを組み込んで、こうした反応速度パラメータ の最適化を実施する。こうした最適化（最小二乗）は、ループを組んで、繰り返し反応器シミュレータを動作させることを行い、目的関数が最小となるようなパラメータを求める。１回の計算時間が 短ければ、数百回や数千回の繰り返しループは苦痛ではないが、１回が数時間、数十分とかかる計算では、解を得るまでに時間がかかりすぎてしまう。また途中で発散したり、演算エラーで計算が ストップしてしまうことがあると、最適化そのものが実行できなくなる。

反応器の混合モデルについては、反応器モデルを参照して下さい。 反応器の差分法による解法は、有限差分法を参照して下さい。

以下、化学プラントの反応器として頻繁に利用される触媒充填固定床型反応器（管型、塔式で定常、一次元）のタイプで、 気相または液相の均一相反応器のシミュレーションを、差分法により行うときの解法手順を詳述する。 初期条件および境界条件を含めた微分方程式系をメッシュ分割点での値を使った離散化をするときの基礎を解説した。本節では具体的な例をあげ、定式化するときの注意事項を述べる。

先頭に戻る

反応器シミュレータの開発ステップ

反応器シミュレーションを開発するときの大まかな手順を以下概観する。

反応器シミュレータの役割

ここで言う反応器シミュレータは、有限差分法や有限要素法を用いてNavier-Stokes式を解く流体解析(CFD)ツールではなく、あくまでも反応成績を簡便に予測するツールを指し、運動方程式を解かずにせいぜい物質収支式や熱収支式を解くツールを指す。市販のプロセスシミュレータ（例えばPro/2、Aspenなど）にも、反応器を解くユニットが用意されているが、反応器モデルが限定されていたり、反応速度式の形が複雑なときにはユーザールーチンを自作しなければならないなど、設計用のツールとして実用上問題があることが多い。そのため、プロセス開発と同時に専用の反応器シミュレータを作成し開発することが多い。

実際のラボスケールやベンチ・パイロットスケールでの反応器開発に伴い、反応速度解析（反応速度定数をフィッティング）を実施するときのツール、および得られた反応速度定数を用いた運転条件を机上で最適化するためのツールを考える。入口の条件（入口ストリームの流量、組成、温度、圧力）を与え、反応器形状や反応器の運転条件を入力として与え、反応器出口のストリームがどうなるかを予測・推算するツールと考える。いわゆる操作型のシミュレータを想定する。

シミュレーション・モデルの作成

前述したシミュレータの役割を満たすに足りる精度のシミュレーション・モデル（反応器設計開発を目的とする場合には化学反応モデルおよび流れ・混合を考慮した反応器モデル）を作成しなければならない。シミュレーション・モデルとは解くべき支配方程式（基礎方程式）を数学的に記述することに相当する。

作成した基礎方程式は、計算機を使って解くことができる必要がある。基礎方程式をコンピュータの言語に変換するプログラミング作業が必要となる。プログラミング作業は単純な数学演算をコードに変換するだけでなく、モデル全体を俯瞰し、効率よく、安定した解が得られるような総合的な知見・経験を必要とする。 実際の反応器シミュレーションは非線型方程式を解く収束計算となることが多く、またその収束性は千差万別で「トライしてみないと分からない」という場合が多い。

反応モデルや混合モデルを組み込んだ反応器シミュレータが開発されると、反応器設計に必要な情報を机上で検討し得ることができる。例えば反応器形状を最適設計したり、最適な運転条件を探索したり、また感度解析を通して運転変動の影響を予測することができる。こうしたプロセス上のリスクや影響に対し予め対策を講ずることにより失敗のない反応器を設計することができる。

先頭に戻る

シミュレータの検証

通常、反応器シミュレータが完成するとその検証作業が行われ、その反応器モデルがカバーできる範囲を確認する。検証は主にスケールアップしたときの混合モデルや反応速度定数の追従性を確認する。ラボ装置からベンチ・パイロットへのスケールアップ時、ベンチからパイロットへのスケールアップ時、モックアップ試験時などの試験データを利用し、シミュレータの検証・確認を行う。検証の結果ずれが大きいときはモデルのブラッシアップ・改良を行い、実装置設計時のリスクをできる限り削減しておく。

いま反応器シミュレータを開発するに当たり、反応器周りの物質収支式および熱収支式を効率よく解くことを考える。いくら厳密なモデリングを行っても、それを解くのに多大な費用・労力・時間を要するならそのモデルは使い物にならないし、逆にあまりにモデルを簡略化しすぎてしまうと、単純な物理現象すらトレースすることができず、スケールアップの役に立たないことにもなる。

先頭に戻る

シミュレータの改良・修正

プロセス開発の初期段階では、反応速度解析のためのツールとして、反応器を簡単なモデルで近似しシミュレータを開発する。これが原型となり、プロセス開発とともにブラッシアップ、改良を加えつつ、実装置設計に耐える反応器シミュレータに完成させることになる。

反応器シミュレータの開発は、反応モデルおよび混合モデルを考慮し、解くべき基礎式を導出することから始まる。基礎式には、成分の物質収支式、総括の物質収支式、熱収支式、ときには圧力収支式がある。均一系反応器では、これら基礎式はひとつの相の収支式でよいが、不均一系（例えば、気液、液液系）反応器のときは、相毎に基礎式が必要となる。

先頭に戻る

不均一系反応のシミュレーション例

不均一系反応の例として図１に示す気液二相系のガス吸収反応器を考えると、成分物質収支は次の３つの収支が考えられる。

図１：気液二相系の物質収支

(a) 気相のＡ成分の物質収支式
(b) 液相のＡ成分の物質収支式
(c) 気液両相のＡ成分の物質収支式

(a)、(b) の物質収支式には、相間の物質移動項が現れるが、(c) の収支式では物質移動項が相殺され現われない。(c) の気液両相の収支式は(a)と(b)の和で表されるため、実際に両相の成分濃度を求めるための基礎式はこの３つのうちどれか２つを使う（３つを使うと式を与えすぎとなり解けない）。ガス吸収反応器のように相間の物質移動項がほかの項に比べ大きいとき、(c) の気液両相の物質収支式を２つのうちのひとつとして採用すると解き易いこともある。総括の物質収支式や熱収支式も、同様に３つ収支式があり、このうちどれか２つを使う。

反応器シミュレータの作成にあたり、解くべき基礎式・境界条件を明らかにし、未知数（独立変数）の数と式の数とが過不足ないように問題を設定しなければならない。

開発当初はできるだけ単純なモデルとし、機能を限定し、ラボ試験データやパイロット試験データのトレースに用い、徐々にモデルを改良・ブラッシアップした方が全体を通じて効率的なシミュレータ開発ができる。また、モデルの基礎式の導出や前提条件を使用説明書として文書化し、残しておくとシミュレータの保守やモデルの改良に役立つ。

先頭に戻る

基礎方程式

定常状態の、一次元触媒充填管型反応器を、混合拡散モデルを用い、基礎方程式を導出し、基礎方程式およびその境界条件を離散化し、非線形連立方程式系に変換することを考える。 取り扱う相はガス相だけを考慮する。また反応はガス成分が固相の触媒により反応する不均一系反応と、気相中でガス分子が衝突しガス相で反応する均一系反応の２つを考慮する。 管外部はある平均温度の流体を流すことにより反応熱の除加熱を行う。

また固定層の途中に、ガスをサイドフィードできることを想定し、基礎式を考える。

基礎式の導出にあたり、次の前提条件を仮定した。

先頭に戻る

成分の物質収支

物質収支として、成分の物質収支式、および総括の物質収支式（または質量保存則）を考慮する。

成分の物質収支式は、
\[\begin{align} 非定常項による成分の蓄積項 & ＋移流項 \\ & = 拡散項＋反応項＋相間の物質移動項 \tag{1} \end{align} \] で表される。

成分物質収支式は成分の数だけ存在し、連立して解くことになる。例えば、３次元の直交座標系の混合拡散モデルで成分の物質収支式は、 \[ \begin{align*} \underbrace {\frac{\partial C_A}{\partial t}}_{蓄積項} & + \underbrace { \biggl( u_x \frac{\partial C_A}{\partial x} + u_y \frac{\partial C_A}{\partial y} + u_z \frac{\partial C_A}{\partial z} \biggr) }_{移流項} \\ & = \underbrace { E \biggl( \frac{\partial C_A^2}{\partial x^2} + \frac{\partial C_A^2}{\partial y^2} + \frac{\partial C_A^2}{\partial z^2} \biggr) }_{拡散項} + \underbrace {R_A}_{反応項} + \underbrace {N_A}_{物質移動項} \tag{2} \end{align*} \]

となる。ここで混合拡散係数 E は空間 (x, y, z) に依存せず、また濃度 CA に独立であるという前提条件を用いた。連続操作で定常問題のとき蓄積項をゼロと置いたり、流れ方向たとえばｚ方向のみの濃度分布が欲しいとき移流項や拡散項の x微分項および y微分項をゼロと置いたり、プラグフローモデルのときは拡散項をゼロとする（拡散係数がゼロ）など、できるだけ基礎式を簡略化することが必要である。モル濃度 CAの代わりにモル分率や重量分率で記述することもできる（ただし単位変換の係数が各項に必要となる）。

先の前提条件を当て嵌める。 左辺は移流項、右辺第１項は拡散項、第２項は触媒による不均一相反応項、第３項は均一相反応項、 第４項はサイドフィード項。 S は反応器容積当たりのサイドフィード容積流量とする。触媒層は重量分率 \( w_k \) の触媒kが充填されている。右辺第２項以下は考える反応モデル次第でもっと単純化可能である。 BC1はDanckwertsの入口境界条件、BC2は出口拡散フラックスゼロの境界条件である。 \[ \begin{align*} \frac d{dz}(uC_i) & = E_z \frac{d^2C_i}{dz^2} + \rho_B \sum_{k,{\rm hetero}} \frac {w_k}{\rho_k} r_k \, \alpha_{k,i} + \varepsilon \sum_{k,{\rm homo}} r_k \, \alpha_{k,i} + SC_{i,s} \tag{3} \\ {\rm BC1: at} & ~ z=0, ~ -E_z \frac {dC_i}{dz}=u(C_{i,{\rm in}}-C_i) \tag{4} \\ {\rm BC2: at} & ~ z=L, ~ \frac {dC_i}{dz}=0 \tag{5} \\ \end{align*} \]

先頭に戻る

総括の物質収支（質量保存則）

総括物質収支式は、モル濃度ではなく質量濃度で表した成分物質収支(3)式の両辺の、全成分で総和を採った式となる。
\[ 非定常の蓄積項 ＋ 移流項 ＝ 拡散項 ＋ 相間の物質移動項 \tag{6} \] ここで反応項が消えるのは、反応の前後で質量は不変であるためである。また成分物質収支(3)式を例えば重量分率やモル分率で表わし、和を取った総括物質収支式と分率の総和の定義式 \[ \begin{align*} \sum_i x_i = 1 \tag{7} \end{align*} \]

とは、式がダブることになる。未知数の数に比べ式の数が多くなり数学的に不定となる。このときは総括物質収支 (8)式か (7)式の定義式のどちらか一つでよい。

シミュレータ作成上、不均一系反応器ではすべての相に対し同じ混合モデルとする必要があり、相毎の混合の違いをモデルパラメータの値で調整することになる。例えば、気泡塔のとき気液ともに混合拡散モデルとして反応シミュレータを組んでおき、例えばガス側をプラグフローで近似するときは混合拡散係数をゼロと入力することで、それぞれの相の流れの違いを表現する。

物質収支に限らず反応にかかわる項はその符号（±）の付け方に注意を払う必要がある。化学量論数αは、原系（原料）のとき負の値を、生成系のとき正の値をとる。また反応熱ΔＨｒ は発熱反応であれば負の値を、吸熱反応であれば正の値をとる。反応速度rＡ の定義の仕方（成分Ａを消費する速度か、生成する速度か、非等モル反応のときどの成分基準の反応速度なのか）にも注意し基礎式を導出する。また相間の物質移動・熱移動項も移動の方向に注意し符号をつける必要がある。

同じく、成分物質収支式の成分和をしたものを総括物質収支とし、質量保存則となる。 反応の前後の重量は不変であり、反応項は質量収支をとると消去される。 ρは流体密度、Sは反応器容積当たりのサイドフィード容積流量。BC1は、 入口での総流入質量フラックスを示す。 \[ \begin{align*} \frac d{dz}(u \rho) & = S \rho_s \tag{8} \\ {\rm BC1: at} & ~ z=0, ~ u \rho = u_{\rm in} \rho_{\rm in} \tag{9} \\ \end{align*} \]

先頭に戻る

熱収支（エネルギー保存則）

非等温、断熱反応のときには、反応熱により反応器内部に温度分布ができる。温度分布を求めるには、熱収支式（エネルギー収支式）を解かなければならない。シミュレータを作成するとき、熱収支式で採用する混合モデルは、物質収支と同じモデルを適用する。熱収支用のモデルのパラメータを適宜選択することにより、実質的なモデルを物質収支のモデルと変えることができる。

反応速度定数にArrhenius型の温度依存性が含まれており、温度に関し強い非線形性を示す（反応項の非線形性は後出する）。そのため反応器シミュレータでは、解の収束安定性を向上させるため、物質収支式と熱収支式とを同時に連立して解くことが多い。 熱収支式は、物質収支式と同様に、
\[ \begin{align*} 非定常の蓄積項＋移流項 & = 拡散項＋反応項＋相間の物質移動に伴う熱移動 \\ & + その他移動項 \tag{10} \end{align*} \] で表される。３次元直交座標系の混合拡散モデルとすると \[ \begin{align*} \underbrace {\rho c_p \frac{\partial T}{\partial t}}_{蓄積項} & + \underbrace { \rho c_p \biggl( u_x \frac{\partial T}{\partial x} + u_y \frac{\partial T}{\partial y} + u_z \frac{\partial T}{\partial z} \biggr) }_{移流項（対流）} \\ & = \underbrace { \lambda \biggl( \frac{\partial T^2}{\partial x^2} + \frac{\partial T^2}{\partial y^2} + \frac{\partial T^2}{\partial z^2} \biggr) }_{拡散項（伝導）} + \underbrace {R_A \Delta H^r}_{反応項} + \underbrace {N_A \Delta H^p}_{物質移動項} \tag{11} \end{align*} \]

となる。ここで、密度ρ、比熱Cp である。拡散項の有効熱伝導度λは空間 (x,y,z) および温度依存性はないという前提条件を用いた。またジャケットなどを通しての熱伝達、輻射伝熱、外気への放熱、相間の物質移動に伴う熱移動の項などは、その他移動項に含めた。

熱収支を表す基礎式もできるだけ簡略化することが望ましい。例えば半径方向の温度分布を考えないとか、軸方向の熱伝導を考えないなど反応器のタイプやシミュレーションの目的により、基礎式を簡略化しないと解くべき方程式が複雑になる。

先の前提条件を当て嵌めたときの熱収支式を示す。左辺は移流項、右辺第１項は拡散項、第２・第３項は反応項、第４項はサイドフィード項、 第５項は壁面での伝熱項、第６項はその他熱ロスを示す。移流項は比熱基準でエネルギー収支をとっているが エンタルピーとして収支式を記述することも可能。

BC1は、入口境界条件で、Danckwerts境界条件、BC2は、出口で熱フラックスがゼロの条件である。 \[ \begin{align*} \frac d{dz}(u \rho c_p^G T) & = \lambda_z \frac{d^2T}{dz^2} + \rho_B \sum_{k,{\rm hetero}} \frac {w_k}{\rho_k} r_k \, (-\Delta H_k) + \varepsilon \sum_{k,{\rm homo}} r_k \, (-\Delta H_k) \\ & + S \rho_s c_{p,s}^G T_s + \frac{S_c}{A}h(T_w-T)+Q_{\rm loss} \tag{12} \\ {\rm BC1: at} & ~ z=0, ~ -\lambda_z \frac {dT}{dz}=u \rho c_p^G(T_{\rm in}-T) \tag{13} \\ {\rm BC2: at} & ~ z=L, ~ \frac {dT}{dz}=0 \tag{14} \\ \end{align*} \]

先頭に戻る

圧力収支

固定床型反応器や触媒充填管型反応器のように、充填層圧損が無視できず、圧力変化により平均流速や平均密度、モル濃度が大きく変化するとき、圧力収支式を同時に解く必要がある。

例えば、触媒充填管型反応器の圧力損失が充填層と流体との摩擦損失のみに支配され、Ergun式で表されるとすると、流れ方向(z方向)の圧力収支式は、 \[ \begin{align*} \frac {dP}{dz} & = -f \frac {\rho u^2}{d_p} \frac 1{g_c} \tag{15} \\ f & =\frac {1-\varepsilon}{\varepsilon ^3}(1.75+150 \frac {1-\varepsilon}{\rm Re} ) \tag{16} \end{align*} \]

となる。チューブ壁面や拡大・縮小部があるときにはこれら項を考慮した圧力収支式を立てる必要がある。

圧力収支として、充填層の摩擦圧力損失のみを考慮する。摩擦損失はErgun式で記述されるものとする。 BC1は、入口境界条件。（圧力微分方程式を解くための境界条件は１点必要であり、出口や途中の１点を指定してもよい。 そのときの差分化はメッシュ点の位置だけが違うことになる。） \[ \begin{align*} -\frac{dP}{dz} & =150 \frac{\mu u}{d_p^2} \frac{(1-\varepsilon)^2}{\varepsilon^3} + 1.75 \frac{\rho u^2}{d_p} \frac{1-\varepsilon}{\varepsilon^3} \tag{17} \\ {\rm BC1: at} & ~ z=0, ~ P=P_{\rm in} \tag{18} \\ \end{align*} \]

先頭に戻る

相間の移動項

不均一系反応器の基礎式を導出するとき、相間の物質移動および熱移動を考慮しなければならない。相間の物質移動には、次のような移動現象がある。

化学プロセスの反応器の中で、気泡塔や通気撹拌槽などのガス吸収反応器が相間の物質移動を含む反応器の例としてよく取り上げられる。物質移動速度NA[kmol/m3/s]は、物質移動係数 [m/s]×界面積 [m2/m3]×濃度差 [kmol/m3] で表され、その単位は反応器単位容積当たり単位時間当たりの移動モル数で表される。

物質移動係数は移動現象ごとにまたは装置形式ごとに多くの相関式が報告されている。特にガス吸収の物質移動速度は、気泡塔のような塔型反応器用、通気撹拌槽用などの相関式が報告されている。ガス吸収以外の移動現象の物質移動係数は便覧類にも載っていない場合が多く、前提条件を設け現象を基礎式に加味することを行う。

先頭に戻る

反応項

物質収支や熱収支に現れる反応項が及ぼすシミュレータ作成上の問題点について述べる。反応器単位体積当たりのＡ成分の反応速度ｒは、 \[ \begin{align*} r = kC_A^mC_B^n \cdots \tag{19} \end{align*} \]

のように反応速度定数ｋ、成分濃度Ci 、反応次数m、nを用い関与する成分の濃度の積で表される。逐次反応、並列反応、複合反応、平衡反応などの複数の反応があるとき、第ｊ番目の反応の化学量論数をαＡｊとし、すべての反応の総和を採ることで、成分Aの総括の反応速度RA（反応によるネットの消費速度）を算出できる。 \[ \begin{align*} R_A = \sum_j \alpha_{A,j}r_j \tag{20} \end{align*} \]

また、第ｊ番目の反応の反応熱をΔHjrとすると、すべての反応により発生する熱量Qは、反応の総和をとり、 \[ \begin{align*} Q = \sum_j r_j \Delta H_j^r \tag{21} \end{align*} \]

で表され、これら反応項が成分収支式や熱収支式に現れる。

反応を含む基礎式を解くときの問題点は、(19)式のようにCAおよびCBが積の形で基礎式に現れ、非線形となることである。反応項がほかの移流項や拡散項に比べ支配的な場合、非線形性が強くなる。通常の反応器設計では転化率として100% 近くを狙っており、反応項が支配的となるケースが大部分を占め、非線型性が強い。

こうした非線形問題を解くとき、単純代入的な繰返し手法（例えば、CBを固定し、CAのみを解き、次に得られたCAを固定し、CBを解く、．．．これを繰り返す）がしばしば用いられるが、収束性は悪く解が得られないことが多い。非線形問題の解法としてNewton法が通常採用される。Newton法を用いCA、CB を同時に連立して解く。また熱収支を同時に解くことも行う。そのため計算に必要なマトリックスが大きくなり、メモリを多く必要とする欠点はあるが、適当な初期値を与えることにより解近傍で二次関数的な収束性を示し、収束安定性も優れている。計算機メモリを効率的に使うため、マトリックス要素をバンドマトリックス（帯行列）にすることで、必要メモリを削減することも行う。

Newton法で成分物質収支式を解くときのもうひとつの問題点は、収束途中に負組成が現われ、反応項が負のべき乗計算となり、計算を継続することができなくなることがある。安定した収束を確保するため緩和係数を導入したり、特別な負組成処理を施す必要がある。

連立の非線型方程式をNewton法で解くときの負組成処理などはここ、数値解析：非線型方程式を参照。

先頭に戻る

離散化

解析領域をN分割し、入口を点O、出口を点Nとする。メッシュ点ｊでの従属変数の値を下付き添字ｊで示す。添字ｊのない変数は解析領域内で一定値をとることを意味する（例えば混合拡散係数、有効熱伝導度など）。

成分iの物質収支（Component Material Balance）

格子点jの離散化式を次式で示す。移流項を風上差分で表現するための収束コントロール用パラメータ \( \delta_M \) を導入している。\( \delta_M=1 \) のとき風上差分に、\( \delta_M=0 \) のとき風下差分に、\( \delta_M=0.5 \) のとき中心差分になる。また収支式として \( M_{i,j} \) を導入しこの値がゼロとなる未知数を求めることになる。 \[ \begin{align*} M_{i,j} & \equiv - \delta_M \frac {u_{j}C_{i,j}-u_{j-1}C_{i,j-1}}{z_{j}-z_{j-1}} -(1- \delta_M) \frac {u_{j+1}C_{i,j+1}-u_{j}C_{i,j}}{z_{j+1}-z_{j}} \\ & + \frac{2E_z}{z_{j+1}-z_{j-1}} \biggl\{ \frac{C_{i,j+1}-C_{i,j}}{z_{j+1}-z_{j}} - \frac{C_{i,j}-C_{i,j-1}}{z_{j}-z_{j-1}} \biggr\} + \rho_B \sum_{k,{\rm hetero}} \frac {w_{k,j}}{\rho_{k,j}} r_{k,j} \alpha_{k,i} \\ & + \varepsilon_j \sum_{k,{\rm homo}} r_{k,j} \, \alpha_{k,i} + \delta_j S C_{i,s} = 0 \quad (j=1,N-1)(i=1,M) \tag{22} \end{align*} \]

BC1での離散化式は次式となる。 \( C_{i,{\rm in}} \) は流入ストリームのモル組成（Given）である。 \[ \begin{align*} M_{i,0} & \equiv E_z \frac{C_{i,1}-C_{i,0}}{z_{1}-z_{0}} +u_0(C_{i,{\rm in}}-C_{i,0})=0 \quad (i=1,M) \tag{23} \end{align*} \]

図２：出口境界の仮想点

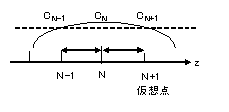
BC2での離散化式は、図２に示すように N点の外側に、N-1点までの距離と同じ距離の仮想点N+1を考え、N点の一階微分ゼロすなわち中心差分をゼロとみなす。 すなわち、仮想点N+1での濃度と、N-1での濃度は等しいと考え、上の(22)式をj=Nとし、（24）式を代入することで第N点での離散化式(25)を得る。 \[ \left. \eqalign{ \begin{align*} & C_{i,N+1}-C_{i,N-1} =0 \cr & C_{i,N+1} =C_{i,N-1} \cr \end{align*} } \right\} \tag{24} \] \[ \begin{align*} M_{i,N} & \equiv \frac{E_z}{z_{N}-z_{N-1}} \biggl\{ \frac{C_{i,N-1}-C_{i,N}}{z_{N}-z_{N-1}} - \frac{C_{i,N}-C_{i,N-1}}{z_{N}-z_{N-1}} \biggr\} + \rho_B \sum_{k,{\rm hetero}} \frac {w_{k,N}}{\rho_{k,N}} r_{k,N} \alpha_{k,i} \\ & + \varepsilon_N \sum_{k,{\rm homo}} r_{k,N} \, \alpha_{k,i} + \delta_N S C_{i,s} = 0 \quad (i=1,M) \tag{25} \end{align*} \]

ここで、反応項は均一系反応(Homogeneous)と不均一系反応(Heterogeneous)の両方を考慮しているが、反応速度 \( r_{k,j} \) は第k番目の反応がメッシュ点jで起こる反応量を示す。これに量論数 \( \alpha_{k,i} \) を乗じることにより、 成分iが消失したり、生成したりする反応速度が求められる。一般に反応速度 \( r_{k,j} \) は、温度、濃度の関数で表され、これら従属変数の非線形関数となる。 \[ \begin{align*} r_{k,j}={\rm Func} (T_j,C_{1,j},C_{2,j},\cdots,C_{M,j}) \tag{26} \end{align*} \]

成分収支式 \( M_{i,j} \) を変形すると、メッシュ点ｊの点と前後１点の合計３点で表されている。入口、出口境界は片側2点で表されている。反応がないときには、成分収支式は次のように線形連立方程式系に変換される。 \[ \left. \eqalign{ \begin{align*} M_{i,0} & = b_0C_{i,0} +c_0C_{i,1} +d_0 &=0 \cr M_{i,j} & = a_jC_{i,j-1} + b_jC_{i,j} +c_jC_{i,j+1} +d_j &=0 \cr M_{i,N} & = a_NC_{i,N-1} + b_NC_{i,N} +d_N &=0 \cr \end{align*} } \right\} \tag{27} \]

この連立方程式の係数行列は、三角行列（Tridiagonal Matrix）となっている。ただし、係数 \( a_j,b_j,c_j \) には流体の線速度 \( u_j \)が含まれており、物質収支だけを計算するときには線速度 \( u_j \)を仮定しなければならない（単純代入的な収束計算が必要となる）。

一方、反応が含まれるとき、第k番目の反応を単純なAとBの反応と考え、\( r_{k,j}\alpha_{k,i}=k_{k,j}C_{A,j}C_{B,j} \) とすると、上の成分Aの収支式 \( M_{A,j} \) の係数 \( b_j \) に速度項以外に \( k_{k,j}C_{B,j} \) の項が含まれることになり、 非線形連立方程式となる。単純代入的に \( u_j,T_j,C_{B,j},\cdots,C_{M,j} \) を仮定し、成分Aの収支を線形連立方程式とみなし解き、収束計算とすることも可能であるが、非線形性が強い系では発散する（今までの経験では、大部分が発散してしまう、注１）。

【注１】基本的に化学反応を取り扱うとき、非線形性は極めて強く、単純代入的な収束手法を始めから選択すべきではない。後述するように、他成分や他変数（線速度、温度、圧力など）と連立して解く方が収束性がよい。

先頭に戻る

総括物質収支（質量保存則）（Overall Material Balance）

質量保存則も、風上差分の収束コントロールパラメータ \( \delta_O \) を導入し、離散化する。 \[ \begin{align*} O_{j} & \equiv \delta_O \frac {u_{j}\rho_{j}-u_{j-1}\rho_{j-1}}{z_{j}-z_{j-1}} +(1- \delta_O) \frac {u_{j+1}\rho_{j+1}-u_{j}\rho_{j}}{z_{j+1}-z_{j}} = 0 \quad (j=1,N-1) \tag{28} \end{align*} \]

BC1では \[ \begin{align*} O_0 \equiv u_0 \rho_0 - u_{\rm in} \rho_{\rm in}=0 \tag{29} \end{align*} \]

BC2（出口）では、バランス式で \( \delta_O = 1 \) とし、N+1点が出現しないよう差分化し、 \[ \begin{align*} O_N \equiv u_N \rho_N - u_{N-1} \rho_{N-1}=0 \tag{30} \end{align*} \]

となる。

成分収支と同様、メッシュ点ｊの前後３点で表され、線速度 \( u_j \) を未知数とし、連立方程式となり、係数行列はTridiagonal Matrixとなる。密度 \( \rho_j \) の温度依存、組成依存、圧力依存を考えると非線形連立方程式となる。

先頭に戻る

熱収支（エネルギー保存則）(Heat Balance)

エネルギー収支も同様に風上差分の収束コントロールパラメータ \( \delta_E \) を導入し、離散化する。 \[ \begin{align*} E_{j} & \equiv - \delta_E \frac {u_{j}\rho_{j}c_{pj}T_{j}-u_{j-1}\rho_{j-1}c_{pj-1}T_{j-1}}{z_{j}-z_{j-1}} -(1- \delta_E) \frac {u_{j+1}\rho_{j+1}c_{pj+1}T_{j+1}-u_{j}\rho_{j}c_{pj}T_{j}}{z_{j+1}-z_{j}} \\ & + \frac{2\lambda_z}{z_{j+1}-z_{j-1}} \biggl\{ \frac{T_{j+1}-T_{j}}{z_{j+1}-z_{j}} - \frac{T_{j}-T_{j-1}}{z_{j}-z_{j-1}} \biggr\} + \rho_B \sum_{k,{\rm hetero}} \frac {w_{k,j}}{\rho_{k,j}} r_{k,j} (-\Delta H_{k,j}) \\ & + \varepsilon_j \sum_{k,{\rm homo}} r_{k,j} (- \Delta H_{k,j}) + \frac SA h(T_{w,j}-T_j) \\ & + \delta_j S \rho_s c_{ps}T_{s} +Q_{{\rm loss},j} = 0 \quad (j=1,N-1) \tag{31} \\ \end{align*} \]

BC1では、 \[ \begin{align*} E_{0} & \equiv \lambda_z \frac{T_1-T_0}{z_{1}-z_{0}} + u_0\rho_0c_{p0}(T_{\rm in}-T_0)=0 \tag{32} \\ \end{align*} \]

BC2では、成分収支と同様、N+1の仮想点を考え、 \( \delta_E=1 \)とし、 \[ \begin{align*} E_{N} & \equiv \frac{2\lambda_z}{z_{N}-z_{N-1}} \biggl\{ \frac{T_{N-1}-T_{N}}{z_{N}-z_{N-1}} - \frac{T_{N}-T_{N-1}}{z_{N}-z_{N-1}} \biggr\} + \rho_B \sum_{k,{\rm hetero}} \frac {w_{k,N}}{\rho_{k,N}} r_{k,N} (-\Delta H_{k,N}) \\ & + \varepsilon_N \sum_{k,{\rm homo}} r_{k,N} (- \Delta H_{k,N}) + \frac SA h(T_{w,N}-T_N) \\ & + \delta_N S \rho_s c_{ps}T_{s} +Q_{{\rm loss},N} = 0 \quad (j=1,N-1) \tag{33} \end{align*} \]

エネルギー収支も、温度を未知数とし、前後３点の温度で表現される。Tridiagonal Matrixとなる。

なお、断熱反応で温度変化があるときには、こうしたエネルギー収支を差分化した式を解かねばならないが、等温反応や温度プロファイルがあらかじめ与えられるとき（実験データがあるとき）には、エネルギー収支をとる必要はなく、単純に、 \[ \begin{align*} E_j \equiv T_j-T_{\rm spec}=0 \quad (j=0,N) \tag{34} \end{align*} \]

と置くことで、ソースコード上は取り扱うことができる。

先頭に戻る

圧力収支 (Pressure Balance)

収束コントロール用パラメータ \( \delta_B \) を導入し、同様に離散化する。 \[ \begin{align*} B_j & \equiv \delta_B \frac{P_j-P_{j-1}}{z_j-z_{j-1}} +(1-\delta_B) \frac{P_{j+1}-P_j}{z_{j+1}-z_j} + 150 \frac{\mu_ju_j}{d_p^2} \frac{(1-\varepsilon_j)^2}{\varepsilon_j^3} \\ & +1.75 \frac{\rho_ju_j^2}{d_p} \frac{1-\varepsilon_j}{\varepsilon_j^3} = 0 \quad (j=1,N-1) \tag{35} \end{align*} \]

BC1では、 \[ \begin{align*} B_0 \equiv P_0-P_{\rm in}=0 \tag{36} \end{align*} \]

BC2（出口）では、バランス式で \( \delta_B=1 \) とし、N+1点の値が出現しないよう、 \[ \begin{align*} B_N & \equiv \frac{P_N-P_{N-1}}{z_N-z_{N-1}} + 150 \frac{\mu_Nu_N}{d_p^2} \frac{(1-\varepsilon_N)^2}{\varepsilon_N^3} +1.75 \frac{\rho_Nu_N^2}{d_p} \frac{1-\varepsilon_N}{\varepsilon_N^3} = 0 \tag{37} \end{align*} \]

となる。

圧力収支も、Tridiagonal Matrixとなる。なお、圧力収支は気相反応で充填層内圧力が場所により変化すると考え、その影響を考慮するときに必要となる。圧力変化が少ないときは圧力収支をとる必要はない（液相反応のときなど）。

先頭に戻る

離散化方程式系の自由度

以上離散化した連立非線形方程式の未知数と式の数（制約条件の数）を算出する。 メッシュ点の総数は、0からNまでの(N+1)個であることに留意し、また成分の総数Mとすると、表のようになる。

表９：一次元充填層型反応器モデルの自由度
基礎式 バランス式 収支式の数 未知数 未知数の数
成分収支 \( M_{i,j} \) (N+1)*M \( C_{i,j} \) (N+1)*M
総括物質収支 \( O_{j} \) (N+1) \( u_{j} \) (N+1)
熱収支 \( E_{j} \) (N+1) \( T_{j} \) (N+1)
圧力収支 \( B_{j} \) (N+1) \( P_{j} \) (N+1)
総和 \( {\bf y(x)=0} \) (N+1)*(M+3) \( {\bf x} \) (N+1)*(M+3)

未知数の数と、方程式の数とが一致しており、数学的に解くことができる。なお基礎式を解く上で必要な入口における境界条件（モデルによっては出口条件）は与えられるものとし、既知とする。

未知数 \( C_{i,j},u_j,T_j,P_j \) が分かれば計算できる物性値などは独立変数と考えず、従属変数とみなしている。また反応速度 \( r_{k,j} \) も独立変数が 求められれば計算できる量であり、反応速度定数等は既知であるとする。

先頭に戻る

離散化方程式の連立化

個々の収支式自体が既に連立方程式化され、その係数行列はTridiagonal Matrixとなっているが、更にこれら収支式を連立化を行い、巨大な非線形連立方程式にし、こらら収支式を同時に解き、収束安定性を確保する方法を考える。

今、メッシュ点jでの未知数は、 \( C_{i,j}(i=1,M),u_j,T_j,P_j \) のM+3個ある。これら未知数を次のようにベクトル表現する。 \[ \begin{align*} {\bf x}_j=[ C_{1,j},C_{2,j},\cdots,C_{M,j},u_j,T_j,P_j]^T \quad (j=0,N) \tag{38} \end{align*} \]

また、これに相当する保存則の式（以下目的関数という）も、ベクトル表現する。 \[ \begin{align*} {\bf y}_j=[ M_{1,j},M_{2,j},\cdots,M_{M,j},O_j,E_j,B_j]^T = {\bf 0} \quad (j=0,N) \tag{39} \end{align*} \]

右辺はゼロベクトル（要素がすべてゼロのベクトル）である。

さらに、メッシュ点0からN点までのこれら変数ベクトル \( {\bf x}_j(j=1,N) \) と目的関数ベクトル \( {\bf y}_j(j=1,N) \) を部分ベクトルとし、全メッシュ点のベクトル \( {\bf x},{\bf y} \)を作る。 \[ \begin{align*} {\bf x} & = [ {\bf x}_0,{\bf x}_1,\cdots,{\bf x}_N ]^T \tag{40} \\ {\bf y} & = [ {\bf y}_0,{\bf y}_1,\cdots,{\bf y}_N ]^T = {\bf 0} \tag{41} \end{align*} \]

目的関数ベクトル \( {\bf y} \) は、変数ベクトル \( {\bf x} \) を未知数とする非線形連立方程式を構成している。 \[ \begin{align*} {\bf y(x)=0} \tag{42} \end{align*} \]

これは、未知数（N+1）*(M+3)個が、\( {\bf y(x)=0} \) を満足するような解を求める非線形最適化問題に変換されたことになる。目的関数ベクトルの係数行列は、図３に示すように、（M+3）個の正方行列を１つの部分行列とする、Tridiagonal Matrixになる。バンド幅3*(M+3)のバンドマトリックスとなる（計算機メモリ節約できる）。

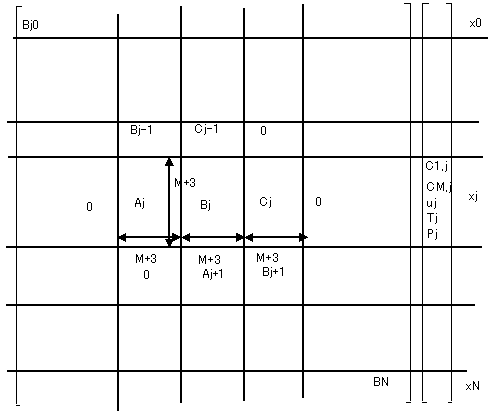
図３：基礎式の係数の構造

先頭に戻る

反応器シミュレーションのまとめ

反応器設計に現れる保存則を示す微分方程式を差分化する方法について、解説した。

反応を伴わない場合にはこれら保存則はほとんどが線形連立方程式で表され、既存ライブラリの線形方程式を解く方法により解を、数値的に求めることができる。また、陽解法を使う時には、収束安定性の制約があり、時間刻み、空間刻みに制限が出てくる。一方、陰解法ではこれら制約は基本的には無くなり、安定した解が得られることがわかる。

反応を伴うときで、陰解法で解くときには、差分化した保存則は非線形連立方程式で表され、これを解くためには、次回にて解説するNewton法などをさらに用いる必要がある。反応を伴う場合には陽解法でも解くことが可能であるが、収束安定性や非線形性の強さにより収束しないことが多い。

演習問題１：

演習問題の解答は、ここ（未リンク）で取り扱っています。

先頭に戻る

Literature Cited

先頭に戻る