トップ > ライブラリ > 数値解析 > ラプラス変換 > ラプラス変換・例題６

数値解析：ラプラス変換・例題６

　現在工事中です。
　ラプラス変換を適用し、工学分野で現れる偏微分方程式を解くことができる。その具体例を 以下に紹介する。ここで示す解析の例題６では、数値解析・ラプラス変換にて解説したラプラス変換の概要を踏まえ、 解析解の式を具体的に導出している。
　本ページでは例題６の、直交座標系の粒子充填層（拡散モデル）の滞留時間分布の問題を取り扱っているが、
　例題５では直交座標系の半無限固体中の非定常伝熱問題を取り扱う。
　例題７では円筒座標系の非定常拡散問題を取り扱う。

先頭に戻る

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

粒子充填層の滞留時間分布（直交座標系）

　直交座標系の非定常の混合拡散モデルの滞留時間分布を求める例題６の解法を以下に示す。
　例題を再掲すると、次のとおり。

例６：触媒充填層の混合拡散モデルL1578),6)

　流体が\(x\)方向に平均流速\(u\)で、軸方向混合拡散係数\(E\)で流れている。ある位置\(x\)ある時間\(t\ \)での成分濃度\(c\ \)の物質収支 式は次式(6-1)で表される。ここで\(\psi(c)\)は反応項を示す。
　初期条件(6-2)式、境界条件(6-3)式とするとき、このモデルの滞留時間分布関数\(E(\phi)\)を求めることを考える。ただし、 反応項\(\psi(c)=0\)とする。初期条件、境界条件はステップ応答実験（当初濃度\(c_0\)の流体を流し、時刻ゼロで濃度ゼロの流体に切り替える）に相当している。\(L\)は反応器長さとする。 \[ \begin{align*} \frac{\partial c}{\partial t}+u\frac{\partial c}{\partial x}= E \frac{\partial^2c}{\partial x^2}+\psi(c) \tag{6-1} \cr \end{align*} \] \[ \begin{align*} \left. \eqalign{ {\rm I.C.} \quad t=0,x>0 : & \quad c=c_0 \cr t=0,x<0 : & \quad c=0 \cr } \right\} \tag{6-2} \end{align*} \] \[ \begin{align*} \left. \eqalign{ {\rm B.C.} \quad x=0 : & -E\Bigl( \frac{dc}{dx}\Bigr)=-uc_s^* \cr x=L : & -E\Bigl( \frac{dc}{dx}\Bigr)=0 \cr } \right\} \tag{6-3} \end{align*} \] ここで\(c_s^*=c_{x \rightarrow +0}\)と表され、層内の濃度分布で\(x=0\)に外挿した値とする。

先頭に戻る

例題６の解法

　本例題は、ラプラス変換を用いた典型的な、しかも多少やっかいな問題である。軸方向の混合拡散モデルの滞留時間分布 を求める、化学工学の分野では古くからの問題で、境界条件から"open vessel"または"closed vessel"などと分類6),7)され、それぞれの解析解5)が導出されている。

ステップ１：基礎式の無次元化

　次の無次元数を導入し、元の微分方程式を無次元化する。 \[ \begin{align*} \theta_T=\frac{L}{u}, \\ \phi=\frac{t}{\theta_T}, \\ {\rm Pe} = \frac{uL}{E}, \\ \bar x=\frac{x}{L},\\ \bar c=\frac{c}{c_0} \end{align*} \] ここで、\(\theta_T\)は平均滞留時間、\({\rm Pe}\ \)はペクレ数である。
　基礎式はつぎのように無次元化される。 \[ \begin{align*} \frac{\partial \bar c}{\partial \phi}=\frac{1}{\rm Pe} \frac{\partial^2 \bar c}{\partial \bar x^2} -\frac{\partial \bar c}{\partial \bar x} \tag{6-4} \end{align*} \] \[ \begin{align*} \left. \eqalign{ {\rm I.C.} \quad \phi=0 : & \quad \bar c=1 \cr {\rm B.C.1} \quad \bar x=0 : & \quad \frac{1}{\rm Pe} \frac{\partial \bar c}{\partial \bar x}=\bar c \cr {\rm B.C.2} \quad \bar x=1 : & \quad \frac{\partial \bar c}{\partial \bar x}=0 \cr } \right\} \tag{6-5} \end{align*} \] 　滞留時間分布をステップ応答実験から求めるには、反応器出口での濃度の時間変化を求め、これを次式のように、時間で微分することで滞留時間分布\(E(\phi)\)を得ることができる。 \[ \begin{align*} E(\phi) &=-\frac{\partial}{\partial \phi} \Bigr(\frac{c}{c_0}\Bigl)_{x=L} \\ &=-\frac{\partial \bar c}{\partial \phi}\biggl|_{\bar x=1} \tag{6-6} \end{align*} \]

先頭に戻る

ステップ２：ラプラス変換による常微分方程式化

　以上で解くための準備が整った。解析解を求めるために、\(\mathcal L \bar c(\phi,\bar x) = C(s,\bar x)\)とラプラス変換する。時間空間を複素空間に変換する。初期条件を適用すると、(6-4)式は次の 常微分方程式(6-7)式に帰する。 \[ \begin{align*} sC-\bar c(0,\bar x)=\frac{1}{\rm Pe} \frac{d^2 C}{d \bar x^2}-\frac{d C}{d \bar x} \\ \frac{1}{\rm Pe} \frac{d^2 C}{d \bar x^2}-\frac{d C}{d \bar x} -sC = -1 \tag{6-7} \end{align*} \] また境界条件もラプラス変換すると、 \[ \begin{align*} \left. \eqalign{ {\rm B.C.1} \quad \bar x=0 : & \quad \frac{1}{\rm Pe} \frac{d C}{d \bar x}=C(s,0) \cr {\rm B.C.2} \quad \bar x=1 : & \quad \frac{d C}{d \bar x}=0 \cr } \right\} \end{align*} \] 　(6-7)式の同次式の特性方程式の根を\(\lambda_1,\lambda_2\)とすると、同次式の解は積分定数を\(A,B\)とすると一般解は次の式となる。 \[ \begin{align*} C &=Ae^{\lambda_1 \bar x}+Be^{\lambda_2 \bar x} \\ {\rm where} \quad \lambda_{1,2} & =U \pm \sqrt{U^2+2sU} \\ U &=\frac{\rm Pe}{2} \\ \end{align*} \] さらに、(6-7)式の非同次式の解を、定数\(D\)として、次の(6-8)式とする。 \[ \begin{align*} C=Ae^{\lambda_1 \bar x}+Be^{\lambda_2 \bar x}+D \tag{6-8} \\ \end{align*} \] (6-8)式を(6-7)式に代入し、整理すると \[ \begin{align*} D=\frac{1}{s} \end{align*} \] を得る。つぎに境界条件を適用し、積分定数\(A,B\)を導出する。 \[ \begin{align*} {\rm B.C.1} \quad & \frac{1}{\rm Pe} (A \lambda_1+B \lambda_2)=A+B+\frac{1}{s} \cr {\rm B.C.2} \quad & A \lambda_1 e^{\lambda_1} +B \lambda_2 e^{\lambda_2}=0 \cr \end{align*} \] この線形連立方程式を解くと、 \[ \begin{align*} A & = \frac{1}{\rm Det} \frac{1}{s} \lambda_2 e^{\lambda_2} \cr B &= -\frac{1}{\rm Det} \frac{1}{s} \lambda_1 e^{\lambda_1} \cr & {\rm where} \quad {\rm Det}=\Bigr( \frac{\lambda_1}{\rm Pe}-1\Bigl)\lambda_2 e^{\lambda_2} -\Bigr(\frac{\lambda_2}{\rm Pe}-1\Bigl)\lambda_1 e^{\lambda_1} \cr \end{align*} \]

したがって、複素領域での基礎式(6-7)の解は次式となる。 \[ \begin{align*} C &=\frac{ \lambda_2e^{\lambda_2}e^{\lambda_1 \bar x} -\lambda_1e^{\lambda_1}e^{\lambda_2 \bar x} +\Bigr( \frac{\lambda_1}{\rm Pe}-1\Bigl)\lambda_2 e^{\lambda_2} -\Bigr(\frac{\lambda_2}{\rm Pe}-1\Bigl)\lambda_1 e^{\lambda_1} } { s\Bigr\{ \Bigr( \frac{\lambda_1}{\rm Pe}-1\Bigl)\lambda_2 e^{\lambda_2} -\Bigr(\frac{\lambda_2}{\rm Pe}-1\Bigl)\lambda_1 e^{\lambda_1} \Bigl\} } \tag{6-9a} \cr & = \frac{P(s)}{Q(s)} \tag{6-9b} \end{align*} \] (6-9a)式の分子分母をそれぞれ\(P(s),Q(s)\)と定義する。

先頭に戻る

ステップ３：分母ゼロとなる極の導出

　(6-9)式を逆変換することで、元の方程式の解を得ることができる。逆変換には数値解析・ラプラス変換のところで示した留数定理、Heavisideの展開定理を 利用する。そのためには、分母\(Q(s)\)の極（根）を求めることが必要である。
　\(s=0\ \)は、式の定義から\(\lambda_1,\lambda_2\)が同時にゼロにならないことから、\(Q(s)\)の{ }内はゼロとならず、1位の極（単極）であることがわかる。 いま\(\lambda_1,\lambda_2\)を次のように変形し、\(\delta\)を定義する。 \[ \begin{align*} \lambda_1 &=U+\delta i \\ \lambda_2 &=U-\delta i \\ -\delta^2 & =U^2+2sU \\ \end{align*} \] そして、\(Q(s)\)に代入し、整理する。 \[ \begin{align*} Q(s) & =s\Bigr\{ \Bigr( \frac{\lambda_1}{\rm Pe}-1\Bigl)\lambda_2 e^{\lambda_2} -\Bigr(\frac{\lambda_2}{\rm Pe}-1\Bigl)\lambda_1 e^{\lambda_1} \Bigl\} \\ & =\frac{e^U}{2U}s \cdot 2i \{(U^2-\delta^2)\sin \delta + 2U\delta \cos \delta \} \tag{6-10} \\ \end{align*} \] ここで、次の関係を用いた。 \[ \begin{align*} e^{\delta i}= \cos \delta + i \sin \delta \\ e^{-\delta i}= \cos \delta - i \sin \delta \\ \end{align*} \] (6-10)式の{ }内がゼロとなる根を求めると、 \[ \begin{align*} (U^2-\delta^2)\sin \delta + 2U\delta \cos \delta = 0 \\ \end{align*} \] を満たす\(\delta \)を、\(\delta_n \ (n=1 \sim \infty) \)とすると、 \[ \begin{align*} 2 \cot \delta_n=\frac{\delta_n}{U}-\frac{U}{\delta_n} \tag{6-11} \end{align*} \] を満たす。\(\delta_n\)は\((n-1)\pi \sim n\pi \)の間に存在する。また、\(Q(s)\)の1位の極である。

先頭に戻る

ステップ４：留数の導出

　以上で\(Q(s)=0\)となる極を求めた。
　続いて、(6-9a)式を逆変換するため、これらの極における留数を、Heavisideの展開定理に基づいて求める。
まづ、\(s=0\ \)の単極で、留数は \[ \begin{align*} {\rm Res}[e^{st}C,0]=\frac{P(0)}{Q'(0)}e^0=\frac{P(0)}{Q'(0)}=0 \tag{6-12} \end{align*} \] となる。ここで、\(s=0\)を代入して \[ \begin{align*} \lambda_1 &=2U \\ \lambda_2 &=0 \\ \delta &=Ui \\ P(0) &=-2Ue^{2U}+2Ue^{2U}=0 \end{align*} \] \[ \begin{align*} \end{align*} \] 一方、\(Q'(s)\)を(6-10)式から導出すると、次式となる。 \[ \begin{align*} Q'(s)=\frac{dQ(s)}{ds} & =\frac{e^U}{2U} \cdot 2i \{(U^2-\delta^2)\sin \delta + 2U\delta \cos \delta \} \\ & +\frac{e^U}{2U}s \cdot 2i \{-2\delta \sin \delta +(U^2-\delta^2)\cos \delta + 2U \cos \delta -2U \delta \sin \delta\} \frac{d \delta}{ds} \tag{6-13} \\ & {\rm where} \quad \frac{d \delta}{ds}=-\frac{U}{\delta} \end{align*} \] この式に、\(s=0\ \)を代入し、整理すると \[ \begin{align*} Q'(0)=-2Ue^{2U} \end{align*} \] したがって、\(s=0\ \)の単極の留数は(6-12)式のとおりゼロとなる。

　次に、\(\delta=\delta_n\)すなわち\(s=s_n\)のときの留数を求める。留数は、次式から求めることができる。 \[ \begin{align*} {\rm Res}[e^{st}C,s_n]=\frac{P(s_n)}{Q'(s_n)}e^{s_nt} \tag{6-14} \end{align*} \] まず、\(Q'(s_n)\)を(6-13)式から求める。右辺第１項に\(s=s_n\)を代入するということは、\(\delta=\delta_n\)を代入することに等しく、\(\delta_n\)の定義から、ゼロとなる。 残る右辺第２項は、\(\delta_n\)の代わりに\(\delta\)を使うと、 \[ \begin{align*} Q'(s_n) &= \frac{e^U}{2U}s_n \cdot 2i \{(U^2-\delta^2+2U)\cos \delta -( 2\delta+2U \delta) \sin \delta\} \frac{-U}{\delta} \\ &=\frac{e^Us_n \sin \delta }{2U\delta^2} \cdot i \{(U^2+\delta^2)(U^2+\delta^2+2U)\} \\ &=-\frac{ie^U\sin \delta}{4U^2\delta^2}(U^2+\delta^2)^2(U^2+\delta^2+2U) \tag{6-15} \end{align*} \] となる。

　一方、\(P(s_n)\)は、(6-9a)式の分子に\(s=s_n\)を代入すれば求められる。\(P(s)\)分子の第３項と第４項は\(\delta_n\)が根であることからゼロとなる。したがって、 残りは第１項と第２項となり、代入整理すると、 \[ \begin{align*} P(s_n) &= \lambda_2e^{\lambda_2}e^{\lambda_1 \bar x} -\lambda_1e^{\lambda_1}e^{\lambda_2 \bar x} \\ &= (U-\delta i)e^{U-\delta i}e^{(U+\delta i)\bar x} - (U+\delta i)e^{U+\delta i}e^{(U-\delta i)\bar x} \\ &= -e^Ue^{U\bar x}i \sin \delta(U^2+\delta^2)\{ \frac{1}{U}\cos \delta \bar x + \frac{1}{\delta} \sin \delta \bar x\} \tag{6-16} \end{align*} \] となる。ここで\(\delta_n\)の代わりに\(\delta\)を使った。これらを(6-14)式に代入し、整理すると \[ \begin{align*} {\rm Res}[e^{st}C,s_n]=\frac{4U\delta e^{U\bar x}(\delta \cos \delta \bar x+U \sin \delta \bar x)} {(U^2+\delta^2)(U^2+\delta^2+2U)}\exp(-\frac{U^2+\delta^2}{2U}\phi) \tag{6-17} \end{align*} \] 以上で逆変換のための留数の導出が終わった。上式で\(\delta\)は\(\delta_n\)のことである。

先頭に戻る

ステップ５：ラプラス逆変換

　故に逆変換結果は、留数定理にしたがって、次式のように留数の和として得られる。 \[ \begin{align*} {\mathcal L}^{-1}C &=\bar c=\frac{c}{c_0} \\ &=\sum_{n=1}^\infty \frac{4U\delta_n(\delta_n \cos \delta_n \bar x+U \sin \delta_n \bar x)} {(U^2+\delta_n^2)(U^2+\delta_n^2+2U)}\exp(U\bar x-\frac{U^2+\delta_n^2}{2U}\phi) \tag{6-18} \end{align*} \]

先頭に戻る

ステップ６：滞留時間分布関数の導出

　次に滞留時間分布関数\(E(\phi)\)を求める。定義式(6-6)にあるように、出口\(x=L,\bar x=1\)のときの濃度の時間変化を求める必要がある。 (6-18)式に\(\bar x=1\)を代入し整理する。 \[ \begin{align*} \Bigr(\frac{c}{c_0}\Bigl)_{x=L}= =4\sum_{n=1}^\infty \frac{U\delta_n(\delta_n \cos \delta_n +U \sin \delta_n )} {(U^2+\delta_n^2)(U^2+\delta_n^2+2U)}\exp(U-\frac{U^2+\delta_n^2}{2U}\phi) \tag{6-19} \end{align*} \] となり、残余濃度曲線を得たことになる。これを無次元時間\(\phi\)で微分して \[ \begin{align*} E(\phi) &=-\frac{\partial}{\partial \phi} \Bigr(\frac{c}{c_0}\Bigl)_{x=L} \\ &=2\sum_{n=1}^\infty \frac{\delta_n(\delta_n \cos \delta_n +U \sin \delta_n )} {(U^2+\delta_n^2+2U)}\exp(U-\frac{U^2+\delta_n^2}{2U}\phi) \tag{6-20} \end{align*} \] が得られるL1578)。さらに整理して、 \[ \begin{align*} E(\phi) &=2\sum_{n=1}^\infty \frac{(-1)^{n+1}\delta_n^2} {(U^2+\delta_n^2+2U)}\exp(U-\frac{U^2+\delta_n^2}{2U}\phi) \tag{6-21} \end{align*} \] が得られるL1338,L1342)。なお、(6-20)式から(6-21)式への変形を筆者はいろいろトライアルしたけど その方法が不明である。なお計算機実験によると、次式が成立していることは確認している。 \[ \begin{align*} U \sin \delta_n + \delta_n \cos \delta_n = (-1)^{n+1} \delta_n \tag{6-22} \end{align*} \]

先頭に戻る

解析解の比較チェック

　以上、混合拡散モデルの滞留時間分布\(E(\phi)\)の式の導出が終わった。つぎに、この式を用いて、既往の文献に紹介されている分布との比較を 行った。
　下の図１は、文献L1338に記載された図に、筆者が計算したそれぞれのペクレ数のときの滞留時間分布をMS-Excel上で計算し、 グラフを重ね合わせた図である。\({\rm Pe}\ =0\)のときは、\(E(\phi)=\exp(\phi)\)であり、それ以外は(6.21)式を用いて計算した。 計算に当たり、\(\delta_n\)として100個まで求め、各項が極めてゼロに近くなるまで、総和を求め、\(E(\phi)\)を算出した。
　ペクレ数が大きいとき、Levenspielの近似式などもあるが、(6.21)式で計算している。それゆえか、\({\rm Pe} \ge 37.5\)のとき、\(\phi)が0.2-0.5の部分で 小さなピークが現れている。総和を100までとしたことが起因している。それ以外の部分は概ね、文献の曲線と一致している。

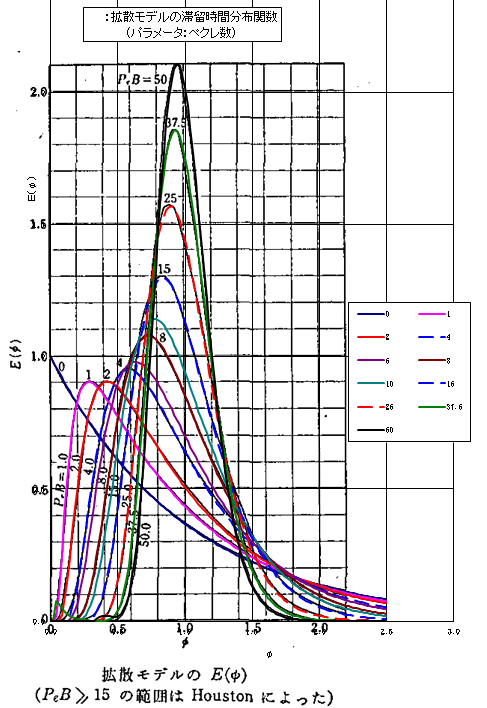
図１：滞留時間分布関数\(E(\phi)\)の比較

　最後の(6.22)式の導出方法が不明であるが、導出した解析解は、文献L1338)に記載する図と一致した。
　式の導出が多少面倒ではあるが、ラプラス変換を利用した偏微分方程式の解析解が得られることが理解されよう。

先頭に戻る

Literature Cited

　本ページを作成するにあたって、以下の書籍を参考にした。

先頭に戻る