トップ > ライブラリ > 数値解析 > ラプラス変換 > ラプラス変換・例題７

数値解析：ラプラス変換・例題７

　現在工事中です。
　ラプラス変換を適用し、工学分野で現れる偏微分方程式を解くことができる。その具体例を 以下に紹介する。ここで示す解析の例題７では、数値解析・ラプラス変換にて解説したラプラス変換の概要を踏まえ、 解析解の式を具体的に導出している。
　本ページでは例題７の、円筒座標系の非定常拡散問題を取り扱っているが、
　例題５では直交座標系の半無限固体中の非定常伝熱問題を取り扱う。
　例題６では直交座標系の粒子充填層（拡散モデル）の滞留時間分布の問題を取り扱う。

先頭に戻る

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

着目成分の非定常拡散方程式（円筒座標系）

　円筒座標系の円柱表面からの蒸発を伴う非定常拡散の解を求める例題７の解法を以下に示す。
　例題を再掲すると、次のとおり。

例７：円柱表面からの蒸発を伴う拡散現象3)

　時刻ゼロで均一の成分濃度\(C_2\)に保たれた、無限長さをもった円柱を考える。その表面から着目成分が蒸発し、時間とともに成分濃度\(C\)が変化する。 円柱自体の形状の時間変化はないものとし、円柱内の濃度分布の時間変化を求める。
　このときの基礎式は、円筒座標系を用い、次の(7-1)式で表される。 \[ \begin{align*} \frac{\partial C}{\partial t}=\frac{1}{r}\frac{\partial}{\partial r}\Bigl( r D \frac{\partial C}{\partial r} \Bigr) \tag{7-1} \end{align*} \] ここで、\(D\ \)は成分の拡散係数で時間・位置には依存しないとする。
　初期条件は、次のように、任意の半径位置で一定の値\(C_2\ \)をもつ。 \[ \begin{align*} {\rm I.C.} \quad t=0,r \ge 0 : \quad C=C_2 \tag{7-2} \end{align*} \] 境界条件は、次のように円柱表面での蒸発を考慮し、また円柱中心の対称性から、 \[ \begin{align*} \left. \eqalign{ {\rm B.C.1} \quad r=a : \quad & -D\frac{\partial C}{\partial r}=\alpha(C_s-C_0) \cr {\rm B.C.2} \quad r=0 : \quad & \frac{\partial C}{\partial r}=0 \cr } \right\} \tag{7-3} \end{align*} \] である。ここで、\(\alpha\ \)は表面蒸発の物質移動係数、\(C_s,C_0\ \)はそれぞれ表面濃度と平衡濃度である。また\(a\ \)は円柱の半径である。
　これら基礎式を初期条件、境界条件にしたがって(7-1)式を解析的に解け。
　さらに、表面からの蒸発量の積算値の時間変化\(M_t\ \)と、無限時間放置したときの蒸発量の積算値\(M_\infty\ \)との比\(M_t/M_\infty\ \)を表す式を導出せよ。

先頭に戻る

例題７の解法

　例題７を解くにあたり、基礎式、境界条件などをまず無次元化し、さらにラプラス変換を用い、常微分方程式に変換し、複素空間での解析解を得る。 その後、逆変換を行い、実空間での解析解を得る。

ステップ１：基礎式の無次元化

　基礎式、境界条件などを次の無次元化濃度\(C^*\ \)を用い、無次元化を行う。 \[ \begin{align*} C^* &=\frac{C-C_2}{C_0-C_2} \\ \end{align*} \]

　無次元化した基礎式、境界条件は \[ \begin{align*} \frac{\partial C^*}{\partial t} & =\frac{1}{r}\frac{\partial}{\partial r}\Bigl( r D \frac{\partial C^*}{\partial r} \Bigr) \\ & = \frac{D}{r} \frac{\partial C^*}{\partial r} + D \frac{\partial^2 C^*}{\partial r^2} \tag{7-4} \\ \end{align*} \] \[ \begin{align*} {\rm I.C.} \quad t=0,r \ge 0 : \quad C^*=0 \tag{7-5} \end{align*} \] \[ \begin{align*} \left. \eqalign{ & {\rm B.C.1} \quad r=a : \quad & -D\frac{\partial C^*}{\partial r}=\alpha(C_s^*-1) \cr & {\rm B.C.2} \quad r=0 : \quad & \frac{\partial C^*}{\partial r}=0 \cr } \right\} \tag{7-6} \end{align*} \] となる。

先頭に戻る

ステップ２：ラプラス変換

　無次元化した成分濃度\(C^*(r,t)\)をラプラス変換し、複素空間での変数\(\bar C(r,s)\)に変換する。 (7-4)式は、初期条件(7-5)式を用いて、 \[ \begin{align*} \frac{d^2 \bar C}{dr^2}+\frac{1}{r}\frac{d \bar C}{dr} -\frac{s}{D}\bar C=0 \tag{7-7} \end{align*} \] と常微分方程式になる。(7-7)式の一般解は、数学公式III1)から、 \[ \begin{align*} \bar C= A J_0(\sqrt{\frac{s}{D}}ir) + B Y_0(\sqrt{\frac{s}{D}}ir) \tag{7-8} \end{align*} \] となる。ここで、\(J_0(x)\)は0次の第１種ベッセル関数、\(Y_0(x)\)は0次の第２種ベッセル関数である。また\(A,B\ \)は積分定数である。
　ベッセル関数は円筒座標系の微分方程式の解として頻繁に現れる。MS-Excelのエンジニアリング関数として組み込まれているので、MS-Excel上で容易にその値を知ることができる。

　境界条件を適用するため、一般解(7-8)を\(r\ \)について微分すると、 \[ \begin{align*} \frac{d \bar C}{dr}= A \Bigr\{-J_1(\sqrt{\frac{s}{D}}ir)\Bigl\} \cdot \sqrt{\frac{s}{D}}i + B \Bigr \{ -Y_1(\sqrt{\frac{s}{D}}ir)\Bigl\} \cdot \sqrt{\frac{s}{D}}i \tag{7-9} \end{align*} \] となる。\(J_1(x),Y_1(x)\)は1次のベッセル関数である。ベッセル関数の微積分の公式は、同じく「数学公式 III」1)に記載されている。 一般解(7-8)式に境界条件(7-6)式を当てはめ、積分定数\(A,B\)を求めることを考える。
　境界条件B.C.2をラプラス変換すると、\(\displaystyle \frac{d\bar C}{dr}=0\ \)となり、 円柱中心\(r=0\ \)では、次のように\(B=0\ \)でなければならない。あるいは、\(\bar C\)の値が円柱中心では有限値でなければならないから、\(B=0\)となる。 \[ \begin{align*} \frac{d \bar C}{dr} & = A \Bigr\{-J_1(0)\Bigl\} \cdot \sqrt{\frac{s}{D}}i + B \Bigr \{ -Y_1(0)\Bigl\} \cdot \sqrt{\frac{s}{D}}i \\ &=0 \\ & {\rm where} \quad J_1(0)=0,Y_1(0)=-\infty \\ & {\rm then} \quad B=0 \end{align*} \]

　残りの境界条件B.C.1をラプラス変換すると、 \[ \begin{align*} -D\frac{d \bar C}{dr}=\alpha (\bar C_s-\frac{1}{s}) \end{align*} \] に変換される。これに、\(B=0\)、(7-8)式、(7-9)式から、\(A\ \)を求めると、 \[ \begin{align*} A=\frac{\frac{\alpha}{s}}{\alpha J_0(\sqrt{\frac{s}{D}}ia)-DJ_1(\sqrt{\frac{s}{D}}ia)\sqrt{\frac{s}{D}i}} \tag{7-10} \end{align*} \] となり、常微分方程式の解析解は最終的に(7-11)式となる。新たに変数\(\beta,L\ \)を導入し、整理すると(7-11b)式となる。 \[ \begin{align*} \bar C & =\frac{\alpha J_0(\beta r/a)}{s \Bigr\{\alpha J_0(\sqrt{\frac{s}{D}}ia)-DJ_1(\sqrt{\frac{s}{D}}ia)\sqrt{\frac{s}{D}i} \Bigl\}} \tag{7-11a} \\ & =-\frac{LJ_0(\beta r/a)}{s\{J_1(\beta)-LJ_0(\beta)\}} \tag{7-11b} \\ & {\rm where} \quad \beta=\sqrt{\frac{s}{D}}ia \tag{7-11c} \\ & \quad \quad L=\frac{a \alpha}{D} \tag{7-11d} \\ \end{align*} \]

先頭に戻る

ステップ３：ラプラス逆変換

　(7-11b)式の逆変換を考える。分子、分母をそれぞれ次のように\(P(s),Q(s)\)とする。 \[ \begin{align*} P(s) & \equiv -L J_0(\beta r/a) \tag{7-12a}\\ Q(s) & \equiv s\{\beta J_1(\beta) - L J_0(\beta)\} \tag{7-12b} \\ \end{align*} \] 分母\(Q(s)\)の{ }内がゼロとなる根\(\beta\)を、\(\beta_n (n=1,2,\cdots \infty)\)とすると、 \(s=0\ \)は単極、\(\beta_n\)も同じく単極となる。\(\beta_n\)は、次式 \[ \begin{align*} \beta_n J_1(\beta_n) - L J_0(\beta_n)=0 \tag{7-12c} \end{align*} \] を満たす。
　\(s=0\ \)の留数は、 \[ \begin{align*} s& \equiv -\frac{\beta^2D}{a^2}=0 ,\quad \beta=0 \\ Res[ e^{st} \bar C,0] &=\frac{-LJ_0(0)e^0}{0J_1(0)-LJ_0(0)}=1 \tag{7-13} \end{align*} \] となる。

　一方、\(\beta=\beta_n\)での留数はHeavisideの展開定理を用いる。そのため\(Q'(s)\)を導出すると \[ \begin{align*} Q'(s) & =\frac{dQ}{ds}=\{\beta J_1(\beta)-LJ_0(\beta)\} +s\{J_1(\beta)+\beta J_1'(\beta)-L J_0'(\beta)\}\frac{d\beta}{ds} \\ &=\{\beta J_1(\beta)-LJ_0(\beta)\}+\frac{\beta}{2}\{\beta J_0(\beta)+LJ_1(\beta)\} \\ & {\rm where} \quad J_1'=J_0-J_1/\beta, \quad J_0'=-J_1 \end{align*} \] となる。ここでプライム"\('\ \)"は\(\beta\ \)による微分を示す。したがって、留数は \[ \begin{align*} Res[ e^{st} \bar C,s_n] &=\frac{-2LJ_0(\beta_n r/a)}{(\beta_n^2+L^2)J_0(\beta_n)} \exp \Bigr(-\frac{\beta_n^2D}{a^2}t \Bigl) \tag{7-14} \end{align*} \] となる。

　故に、逆変換した結果は、留数定理から \[ \begin{align*} {\mathcal L}^{-1}\bar C=C^*=\frac{C-C_2}{C_0-C_2} =1-\sum_{n=1}^\infty \frac{2LJ_0(\beta_n r/a)}{(\beta_n^2+L^2)J_0(\beta_n)} \exp \Bigr(-\frac{\beta_n^2D}{a^2}t \Bigl) \tag{7-15} \end{align*} \] となる。(7-15)式は基礎式の解析解であり、任意の位置、時間での濃度分布を与える。

先頭に戻る

ステップ４：表面からの蒸発量

　次に、表面からの蒸発量の総和を求める。時間無限のときの蒸発量\(M_\infty\)は、円柱内の濃度は至る所で平衡濃度\(C_0\)に到達するから、 初期濃度\(C_2\)からの差が蒸発量の総和となる。一方、任意の時刻\(t\ \)のときの蒸発量\(M_t\)は、円柱内の濃度分布を積分して残留している濃度を 算出する必要がある。なお蒸発量は円柱の単位長さを基準としている。 \[ \begin{align*} M_\infty & =\pi a^2C_2-\pi a^2C_0=\pi a^2(C_2-C_0) \tag{7-16} \\ M_t & =\pi a^2C_2- \int_0^a 2\pi rCdr \tag{7-17} \end{align*} \] 　(7-17)式に、(7-15)式を代入し、積分する。 \[ \begin{align*} M_t &=\pi a^2(C_2-C_0)+2\pi(C_0-C_2) \\ & \quad \sum_{n=1}^\infty \frac{2L}{(\beta^2+L^2)J_0(\beta_n)} \exp \Bigr(-\frac{\beta_n^2D}{a^2}t \Bigl) \int _0^a rJ_0(\beta_n r/a)dr \\ &=\pi a^2(C_2-C_0)+2\pi(C_0-C_2)\sum_{n=1}^\infty \frac{2La^2J_1(\beta_n)}{\beta_n(\beta_n^2+L^2)J_0(\beta_n)} \exp \Bigr(-\frac{\beta_n^2D}{a^2}t \Bigl) \tag{7-18} \end{align*} \] ここで、次の定積分の公式1)を利用した。 \[ \begin{align*} \int_0^a rJ_0(\beta_n r/a)dr & = \Bigr[ \frac{ra}{\beta_n}J_1(\beta_n r/a)\Bigl]^a_0 \\ & = \frac{a^2}{\beta_n}J_1(\beta_n) \end{align*} \]

　比\(M_t/M_\infty\)は、(7-16)式と(7-18)式の比を取って、さらに(7-12c)式の関係を用いて、 \[ \begin{align*} \frac{M_t}{M_\infty}=1-\sum_{n=1}^\infty \frac{4L^2}{\beta_n^2(\beta_n^2+L^2)} \exp \Bigr(-\frac{\beta_n^2D}{a^2}t \Bigl) \tag{7-19} \end{align*} \] となる。本式は、Crankの図書4)の頁80に記載する(5.49)式と一致する。

先頭に戻る

例題の計算例

　与えられた偏微分方程式の解析解が(7-19)式のように得られた。この式に無次元化時間\(Dt/a^2\)における蒸発量変化\(M_t/M_\infty\)を 計算した。MS-Excel上で計算結果を読み込み、MS-Excelのグラフ化機能を用いて、グラフを作成した。結果を、下の図１に示す。凡例に示すように、\(L \equiv a \alpha/D\)をパラメータとしている。
　計算に当たり、\(\beta_n\)を求める必要があり、(7-12c)式から収束計算（Newton法）により、n=1～20までの根を求めた。n=6までの根は 図書3),4)に記載されている。

　Crankの図書4)では、Newmanによる計算結果の値をプロットした図を載せており、図１の下図にCrankの本記載の図を置き、その上に 計算結果を重ねて示している。計算結果でS字カーブの屈曲点で一致がよくないが、グラフ化するときの時間刻みがラフだったのが原因と考えられ、全体的にほぼ重なっているといえる。

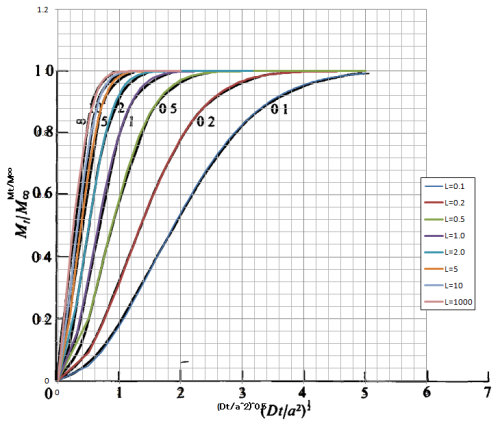
図１：蒸発量の時間変化の計算例

　ラプラス変換を用いて、円筒座標系の非定常拡散方程式の解析解の導出を行った。円筒座標系の偏微分方程式を解くとき、その性質から、 ベッセル関数が頻繁に現れる。ベッセル関数はMS-Excelのエンジニアリング関数として標準で備わっていて、シート上で簡単にその値を知ることができる。

先頭に戻る

Literature Cited

　本ページを作成するにあたって、以下の書籍を参考にした。

先頭に戻る